東京大学
茨城大学

全文PDF

発表概要：

東京大学物性研究所（所長：森初果）の池田達彦助教と茨城大学大学院の佐藤正寛准教授の研究グループは、レーザーなど周期性をもった外場を照射された散逸量子系（注1）の非平衡定常状態（注２、図1）を記述する一般公式を発見しました。レーザー技術は近年猛烈にに進展しており、それらを利用した基礎・応用研究は枚挙に暇がありません。中でも、レーザーの周期電磁場の効果により物質の性質（電気伝導性・磁性・トポロジカル物性・時間結晶など）を高速で変化させることを目指す研究はこの10年間で飛躍的に深化しました。このように周期性をもった外場によって新たな性質や機能を発現させることをフロケ・エンジニアリング（注３、図２）と呼び、最新の高強度レーザーによって実現が可能になってきました。しかし、レーザー中の物質系を含む非平衡系を正確に記述する物理理論を構築するのは一般に困難であり、これまでのフロケ・エンジニアリングについて十分に理論整備されているのは、散逸のない理想的な場合に限られていました。しかし、身の回りのほぼ全ての物質は周りの環境とエネルギーをやり取りし、散逸が常に起きています。そこで、研究グループは、広い散逸のある量子系を表すリンドブラッド方程式（注4）を起点として、高周波展開（注5）と呼ばれる理論手法を応用し、レーザーで駆動された非平衡定常状態を記述する一般公式を導き出しました。

これにより、散逸の効果を取り込んだ定量的なフロケ・エンジニアリングの予言が可能になります。また、本公式は周期駆動された非平衡系の統計力学の足掛かりを与え、非平衡系の基礎科学にも寄与するものです。

本研究成果は国際科学雑誌Science Advancesの2020年7月3日付けオンライン版に公開されました。

発表内容：

① 研究の背景

近年、高強度レーザー技術が著しく進展し、物性科学に新たな潮流が生まれています。その一つが、物質にレーザーを照射することでその状態を変化させ、物質の望ましい性質や機能（電気伝導性・磁性など）を人工的に作り出すという研究の方向性です。特に、レーザー電磁場の時間的な周期振動を利用した物質制御は、フロケ・エンジニアリングと呼ばれ、近年活発に研究が行われています。しかし、レーザーの様な周期外場でどのような物質制御が可能かを判別する一般理論は、これまで散逸のない理想的な孤立系に限られていました。身の回りのほぼ全ての物質は周りの環境とエネルギーのやり取りをしており、散逸の効果（注1）は避けられず、これらの通常の物質を含んだ広範な物理系に適用できる周期駆動系の一般理論は未発達でした（図１）。一方、周期駆動された個別の散逸系においては理論解析が行われてきたものの、高度な計算を必要とし、幅広い対象に適用可能な公式は得られていませんでした。

図 1 非平衡定常状態の概念図
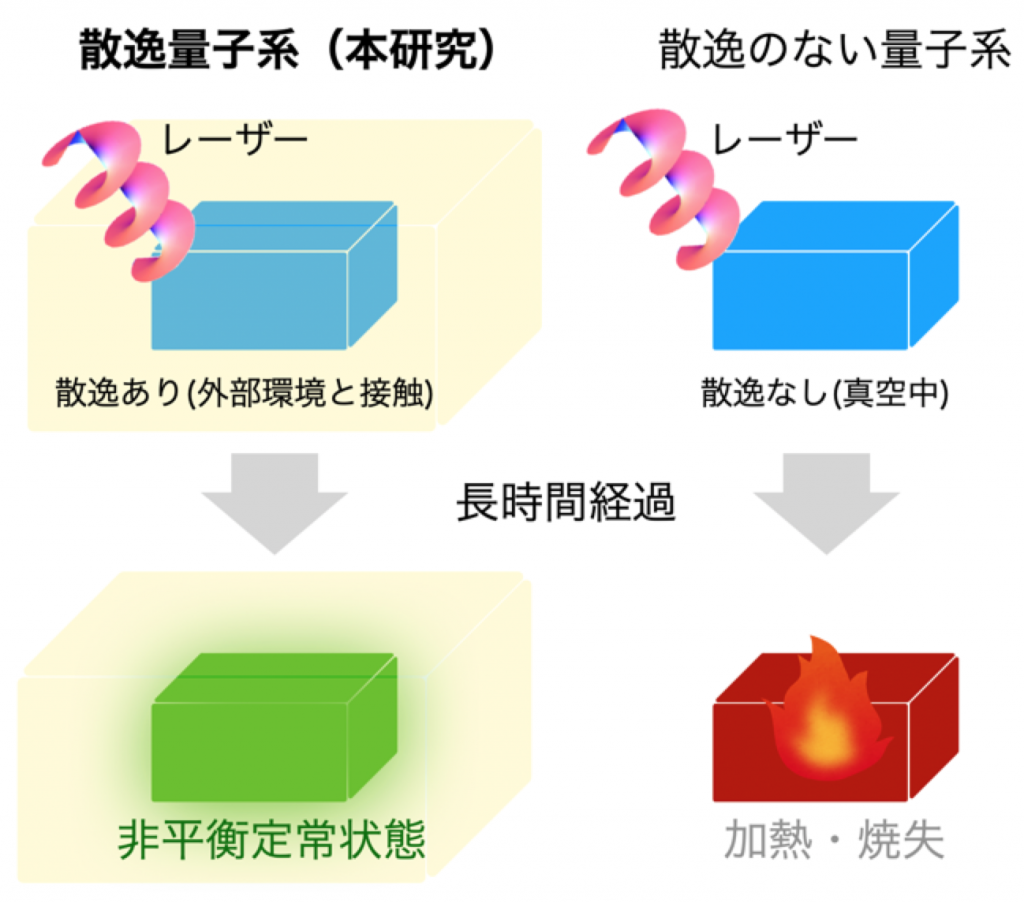
散逸のある量子系は外部環境に余剰エネルギーを排出できるため、長時間のレーザー照射によってエネルギー注入とエネルギー散逸が釣り合った非平衡定常状態に達する。一方、散逸のない量子系では注入されるエネルギーが溜まり、興味深い性質が失われた高温の状態になってしまう。本研究では、散逸量子系の非平衡定常状態の一般公式を構築した。

図 2　フロケ・エンジニアリングの概念図
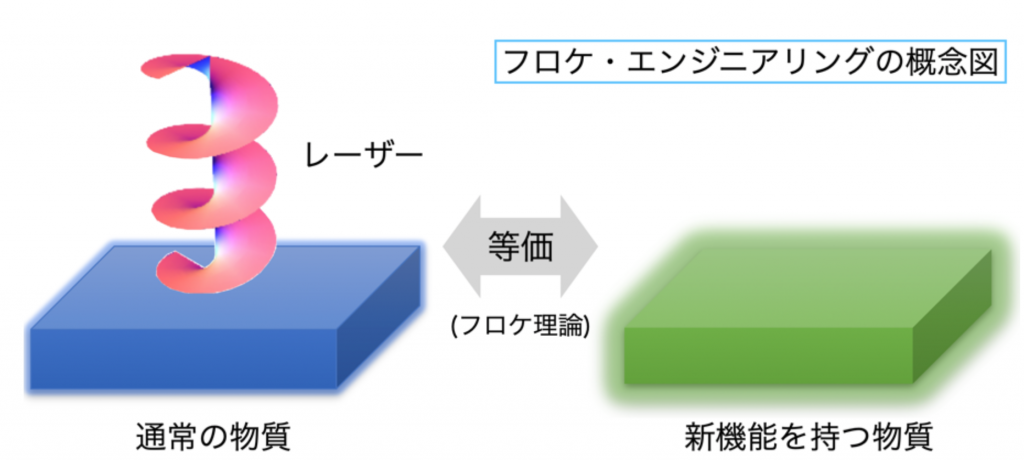
物質にレーザーなどの周期駆動を行う状況は、実効的に新機能を持つ別の物質とみなすことが出来る（フロケ理論）。これをもとに、望む新機能を実現するための物質・レーザーの組み合わせをデザインする方法がフロケ・エンジニアリングと呼ばれる。

② 研究内容

今回、研究グループは、リンドブラッド方程式と呼ばれる広い散逸量子系のダイナミクスを記述する方程式を出発点として、一般的な周期外場中の散逸系の包括的な解析を行いました。散逸のない系で用いられる高周波展開という理論手法をリンドブラッド方程式へ拡張して適用することで、非平衡定常状態を記述する一般的な公式を発見しました。この公式は、レーザー周波数が高い状況において非常に良い精度で非平衡定常状態を記述します。これまでの散逸を含まない理論ではしばしばフロケ・エンジニアされる物理量の値が過大評価されていましたが、今回の公式を応用することで、散逸の効果を取り込んだ物理量の現実的評価が可能となります。また、この公式を用いた状態の計算は非常に簡単で、コンピュータ・シミュレーションに比べて高い実用性があります。

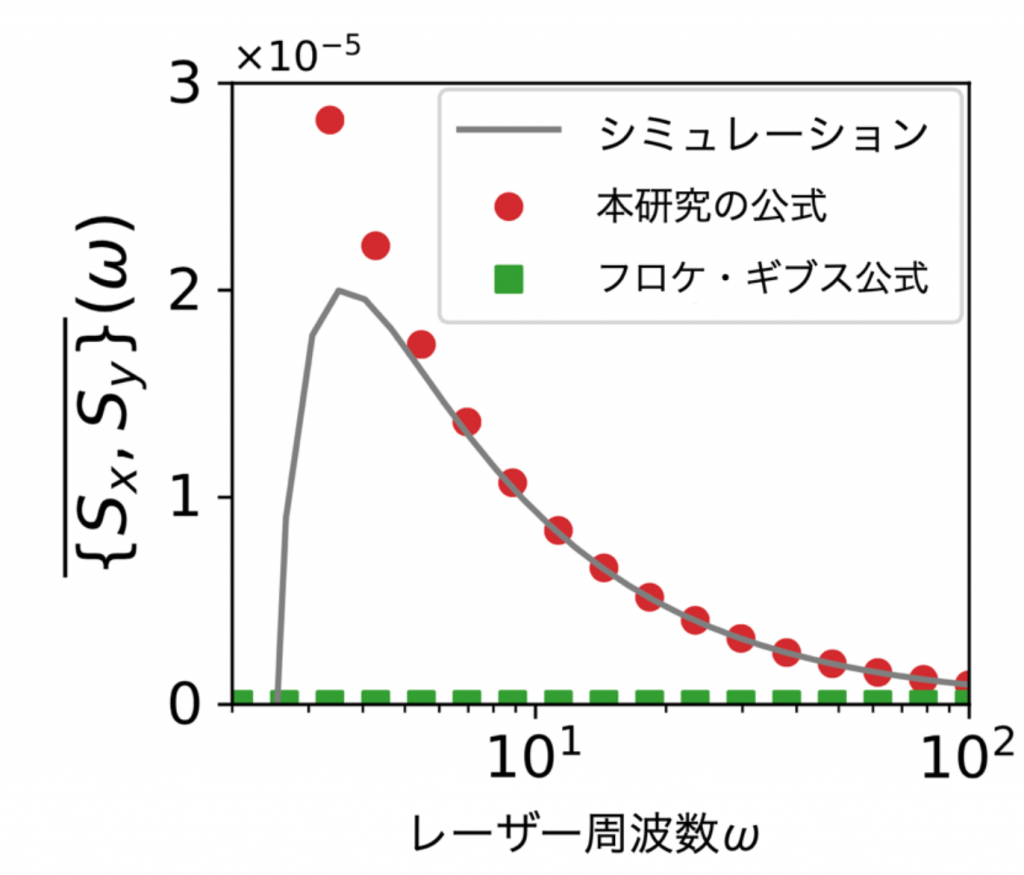
研究グループはダイヤモンドのNV中心（注6）のモデルにおいて、この公式が非平衡定常状態の時間平均・ゆらぎ、及び対称性を正しく再現することを検証しました。その中で、特に散逸のない系では時間反転対称性により禁止される物理量（注7）が散逸の効果によって発現する様子も正しく再現することを明らかにしました（図３）。このことは、散逸系に固有のフロケ・エンジニアリングの可能性を示します。

図 3　ダイヤモンドNV中心における公式の検証
ダイヤモンドNV中心に円偏光レーザーを長時間照射して実現する非平衡定常状態において、時間反転対称性（を含む操作）で禁止される物理量の値を、シミュレーション、本研究の公式、先行研究で提案されていたフロケ・ギブス公式の３つでそれぞれ計算した結果。本研究の公式はレーザー周波数が高い領域でシミュレーションをよく再現する。

③ 社会的意義・今後の予定

レーザーなどの周期駆動によるエネルギー注入と、散逸によるエネルギー流出が釣り合った非平衡定常状態の解析は一般には難しい問題ですが、高周波領域においては本研究成果によってその一般的な解が得られました。このことは、散逸の避けられない実際の物質の性質をレーザーなどで制御するフロケ・エンジニアリングの指針を確立するための第一歩と言えます。これを足掛かりとして、非平衡物理学に関わる基礎・応用研究を進展させることが期待できます。研究グループは、今回の公式をより微視的なレベルへ深化させる基礎科学研究や、本公式による新しいフロケ・エンジニアリングの提案などの応用研究を進めていく予定です。

なお、本研究は、日本学術振興会の科学研究費（課題番号 JP18K13495 , JP17K05513, JP20H01830）、新学術領域研究「量子液晶の理論構築」（課題番号19H05825）の助成を受けたものです。

発表雑誌：

• 雑誌名：「Science Advances」（7月3日オンライン版）
• 論文タイトル：General description for nonequilibrium steady states in periodically driven dissipative quantum systems
• 著者：Tatsuhiko N. Ikeda* and Masahiro Sato*
• DOI：10.1126/sciadv.abb4019

用語解説：

（注１）散逸量子系

真空中の原子など外部環境との接触がほぼ無視出来る量子系が孤立量子系と呼ばれるのに対し、物質中の電子や多くの量子デバイスなどは、外部環境と接触しており、エネルギーの外部環境への散逸が無視出来ない。このように外部環境との接触が無視できない量子系を散逸量子系（または開放量子系）と呼ぶ。

（注２） 非平衡定常状態

駆動（レーザー照射など）に伴って対象系に注入されるエネルギーと、対象系が接触している外部環境へと散逸するエネルギーが釣り合った状態。駆動のない系で長時間後に実現する熱平衡状態と対比される概念。（図1参照)

（注３） フロケ・エンジニアリング

レーザーなどの周期駆動を物理系に照射することで、実効的に新機能（電気伝導性・磁性・トポロジカル物性・時間結晶など）を持った別の物理系を実現する方法。この方法の数学的な基礎である「フロケの定理」の名前が冠されている。（図2参照）

（注４） リンドブラッド方程式

散逸のない理想的な量子系を記述するシュレーディンガー方程式に対して、散逸のある系を記述する方程式の一つ。量子状態が満たすべき数々の性質を全て満たす、数少ない方程式の一つであり、量子光学などで伝統的に用いられてきた。発見者のリンドブラッドの名前が冠されることが多いが、独立な研究で発見した三名の名前を合わせてGKSL（Gorini–Kossakowski–Sudarshan–Lindblad）方程式とも呼ばれる。

（注５） 高周波展開

レーザーの角周波数ωが大きいとき、その逆数1/ωは微小量となる。この微小量を用いて方程式の解を、べき展開（テイラー展開）によって逐次的に高精度に求める理論手法。

（注６） ダイヤモンドのNV中心

炭素原子からなるダイヤモンドの中に存在する格子欠陥の一つ。本来炭素原子がある位置に、窒素原子（N）と空孔（Vacancy）が隣接し、この複合欠陥が量子力学的に振る舞うことが知られている。この量子力学的性質は室温でも持続することから、量子デバイスへの応用などが活発に研究されている。

（注７） 時間反転対称性により禁止される物理量

自然界には、コマの回転など、時間反転（動画を逆再生）すると向きが反対になる様々な物理量が存在する。これらの物理量は、熱平衡状態など時間反転で不変な状態においては、厳密にゼロであることが要請される。

(公開日: 2020年07月04日)