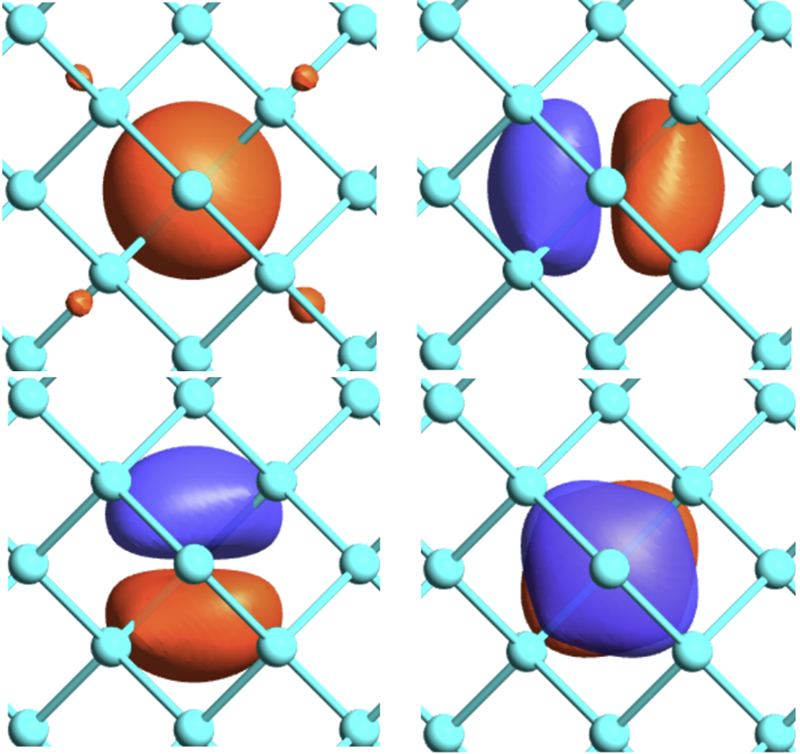
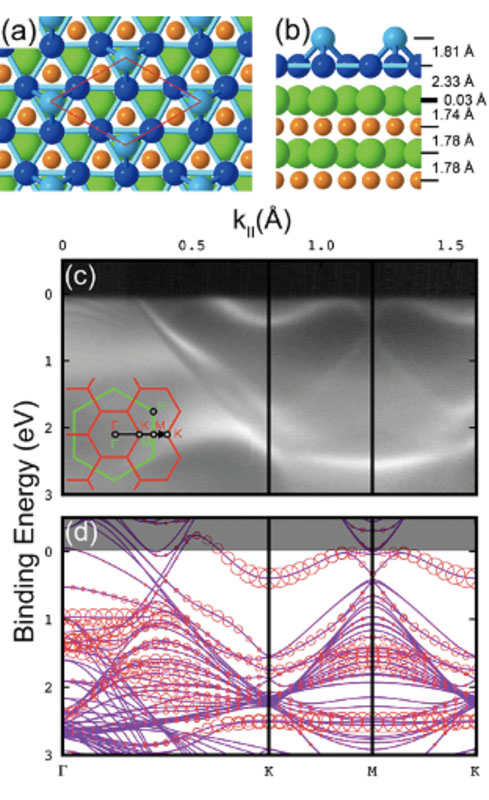
With the development of supercomputers and the refinement of materials science, the importance of first-principles electronic structure calculations has been increasing. We are engaged in developing a new computational method and software package, OpenMX, based on density functional theory, to precisely handle systems close to reality. Based on the versatile atomic-like basis function method, we have developed various efficient computational methods, such as the order-N divide-and-conquer method based on localized natural orbitals, the atom decomposition method by modified recursive bisection, and the Fast Fourier Transform parallelization method with minimal communication volume, enabling simulations that can be directly compared to experiments. Recently, we have been working on the development of calculation methods for the absolute binding energy of core electrons, the closest Wannier function method, machine learning potential methods, and the development of exchange-correlation functionals, aiming for further advances in first-principles calculations. We are also engaged in first-principles simulations of material surfaces and two-dimensional structures, conducting joint research with experimental groups.

• Publications
• Research Highlights