「スキルミオンひも」を用いた信号伝達に成功 -フレキシブルで超低消費電力な新しい情報伝送路の実現に期待-
東京大学
理化学研究所
科学技術振興機構(JST)
発表のポイント
- スキルミオン(注1)ひも(電子のスピン(注2)が作るナノスケールの渦糸構造)の中を振動が伝わる様子を観測することに初めて成功。
- スキルミオンひもは、その直径の1000倍以上の長距離にわたって信号を伝達することができ、順方向と逆方向の伝搬特性が異なるダイオード的な性質を持っていることを発見。
- スキルミオンひもの振動は、電線上の電気信号と異なりジュール損失を生じないことから、フレキシブルで超低消費電力な新しい情報伝送路としての活用に期待。
発表概要:
東京大学大学院工学系研究科の関真一郎准教授(JSTさきがけ研究者兼任)らの研究グループは、スキルミオンひも(磁性体中の電子スピンが作るナノスケールの渦糸構造)を利用した信号伝達を実証することに成功しました。渦巻き状のスピン構造であるスキルミオンは、2次元系では粒子のように振る舞うことが知られており、次世代の情報ビットの候補として近年盛んに研究されています。一方、3次元系のスキルミオンは「ひも」としての性質を持つことがわかっていますが、このスキルミオンひもがどのような応答や機能を示すのか、これまでほとんど明らかにされていませんでした。本研究では、スキルミオンひもの中を振動が伝わる様子を詳細に調べることで、ひもの直径の1000倍以上の非常に長い距離にわたって信号の伝達が可能であること、また順方向と逆方向の伝搬特性が異なるダイオード的な振る舞いが現れることを発見しました。スキルミオンひもの振動は、電線上の電気信号と異なりジュール損失を生じないことから、上記の結果は、スキルミオンひもをフレキシブルで超低消費電力な新しい情報伝送路として活用できる可能性を示しています。
本研究成果は2020年1月14日(火)に英国科学誌「Nature Communications」に掲載されました。
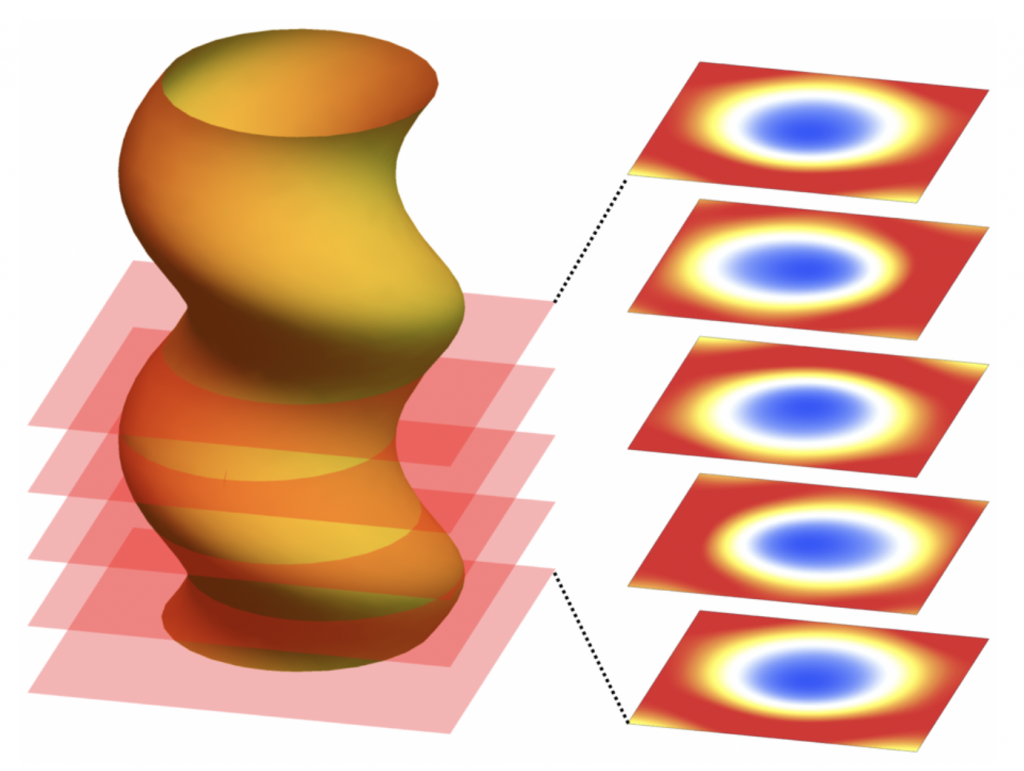
磁性体の中の電子スピンが作る「スキルミオンひも」の中を、振動が伝わっていく様子を示したもの。スキルミオンひもは、幾何学的な性質(トポロジー)によって保護されているために外乱に強いという特徴があり、フレキシブルで超低消費電力な新しい情報伝送路として活用できる可能性が期待されます。
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業個人型研究(さきがけ)の「トポロジカル材料科学と革新的機能創出」研究領域(No. JPMJPR18L5)および「新物質科学と元素戦略」研究領域、日本学術振興会(JSPS)科学研究費補助金基盤研究A(No. 18H03685)、同新学術研究領域「ナノスピン変換科学」(No. 17H05186)の助成を受けて行われました。
発表内容:
■研究背景
近年、物体の幾何学的な特徴を表す「トポロジー(注3)」と呼ばれる概念が、革新的な物質機能を実現するための鍵として大きな注目を集めています。一般に、異なるトポロジーに属する物体は、連続変形で互いに変換することができません。このため、特殊なトポロジーを伴った状態は、外部からの乱れや刺激に対して非常に安定であるという特徴があります。このようなトポロジーに守られた状態としては、例えば磁性体の中の電子のスピンが作り出す「渦」が知られており、2016年にはこうした物質のトポロジカル相の研究に対して、ノーベル物理学賞が与えられています。
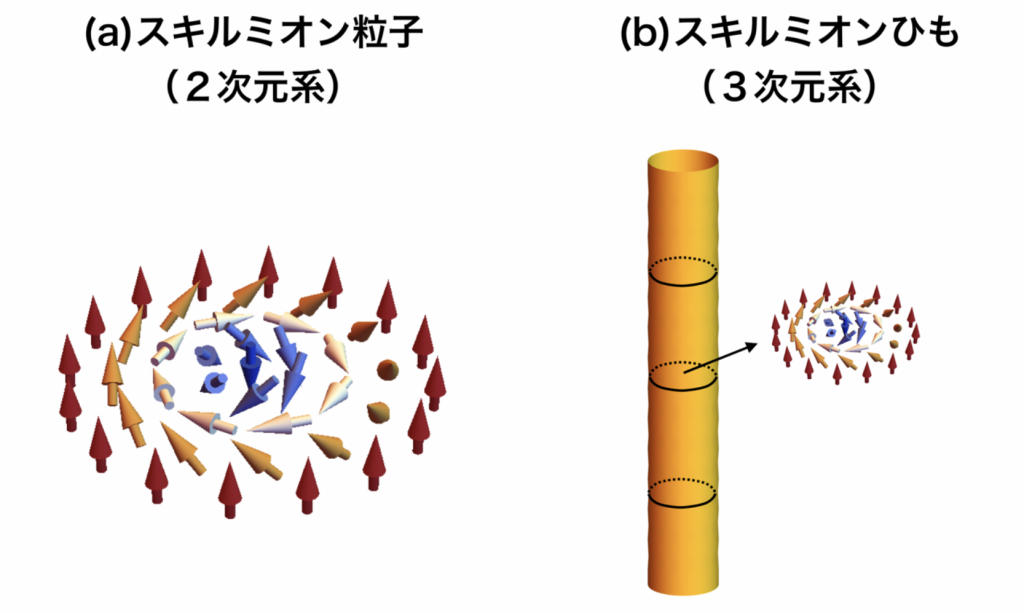
上記のようなトポロジーに守られたスピン渦には、いくつかの種類が存在することが知られており、特に最近注目されているのが、「磁気スキルミオン」と呼ばれる新しいタイプのスピン渦です。スキルミオンは、その構成要素であるスピンを並べ替えると球面をちょうど整数回だけ覆うことができるという特徴をそなえており、薄膜のような2次元系では安定な粒子としての性質を持っています(図1(a))。このスキルミオン粒子は、直径が数~数十ナノメートルと極めて小さく、またさまざまな外場によってその運動や安定性を制御できるため、次世代の磁気記憶・演算素子のための新しい情報ビットの候補として、近年盛んに研究されています。一方、バルク結晶のような3次元系では、スキルミオンは安定な「ひも」としての性質を持つことがわかっています(図1(b))。しかし、このスキルミオンひもがどのような応答や機能を示すのかについては、これまでほとんど明らかにされていませんでした。
■研究内容
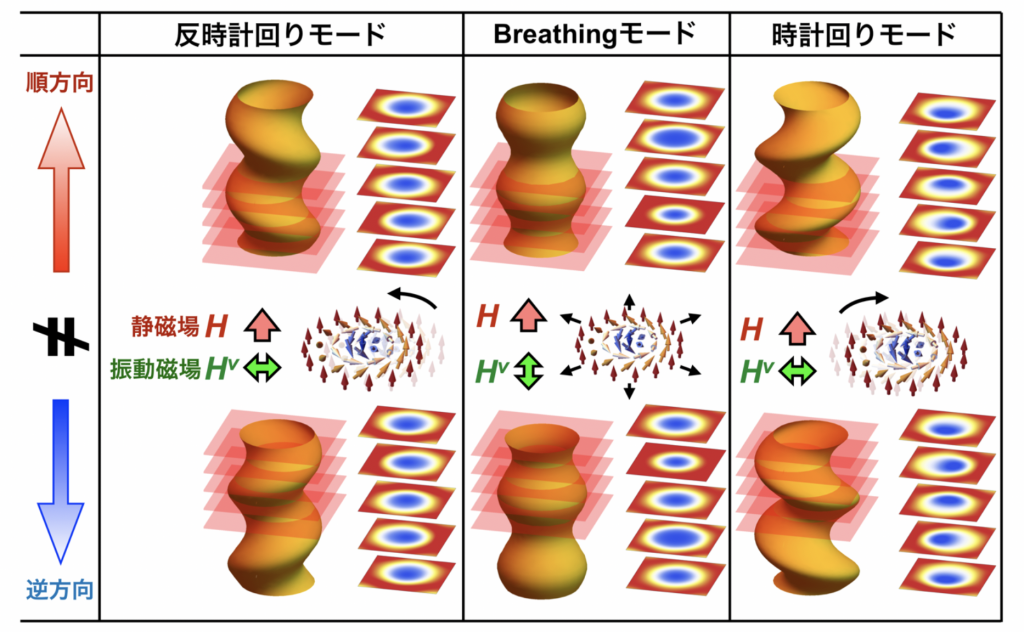
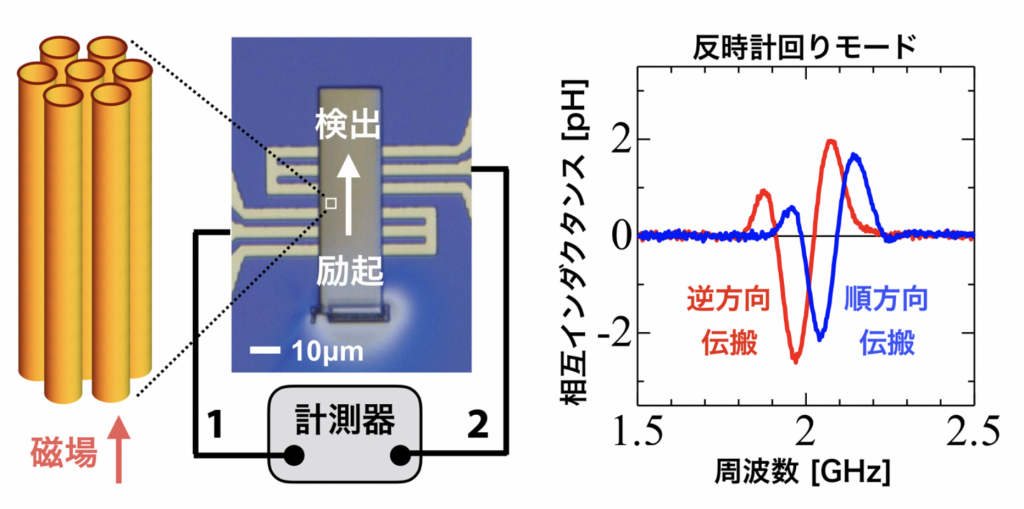
そこで本研究では、スキルミオンひもを用いた情報伝送の可能性を探るため、ひもを揺らした時に振動がどのようにひもの中を伝わっていくのか、実験・理論の両面から明らかにすることを試みました。具体的には、ギガヘルツ帯域の高周波信号を送信・受信するための一対のアンテナ上に、スキルミオンひもを生じることが知られているキラル磁性体Cu2OSeO3の微小結晶を載せて、アンテナ間の相互インダクタンスの測定を行いました。その結果、スキルミオンひもが3つの固有振動モードを持っており(図2)、それぞれ異なる周波数の振動磁場を用いて共鳴励起することで、各モードを介した信号伝送が可能であることを明らかにしました(図3)。さらに詳細な解析の結果、スキルミオンひもがその直径の1000倍以上の非常に長い距離にわたって信号を伝達できること、また順方向と逆方向で異なる伝搬特性が現れる「ダイオード」的な性質を持っていることも発見しました。こうした一連の振る舞いは、微視的な理論計算による予測とも良く一致しています。
■社会的な意義および今後の予定
本研究の結果は、スキルミオンひもを、トポロジーによって守られた強靱でフレキシブルな新しい情報伝送路として活用できる可能性を示しています。電線中の電気信号とは異なり、スキルミオンひもの振動はジュール発熱によるエネルギー損失を生じません。さらに、局所的な磁場や電場を外部から与えることで、スキルミオンひも自体の書き込み・消去を行うことも可能です。こうしたスキルミオンひもの性質を利用することで、動的な書き換えが可能かつ超低消費電力な、ユニークな特徴を持った信号伝送回路・ネットワークを構成できることが期待されます。
また、本研究で取り上げたスキルミオンひも以外にも、自然界ではさまざまなスケールで、トポロジーに守られたひも状の構造が現れることが知られています。これらはしばしば「量子渦」という名前で総称され、代表的な例としては、超伝導体・超流動体で観測される渦糸や、宇宙論の分野で存在が議論されている「宇宙ひも」が挙げられます。これらの系は、互いによく似た性質を示すことが知られており、本研究の結果は、ひも状の構造を持った量子渦の振る舞いの統一的な理解にもつながることが期待できます。
発表雑誌:
- 雑誌名:Nature Communications
- 論文タイトル:Propagation dynamics of spin excitations along skyrmion strings
- 著者:S. Seki*, M. Garst, J. Waizner, R. Takagi, N. D. Khanh, Y. Okamura, K. Kondou, F. Kagawa, Y. Otani, Y. Tokura
- DOI番号:10.1038/s41467-019-14095-0
用語解説:
- 注1)スキルミオン
- スキルミオンは、もともと素粒子物理学の分野でTony Skyrme博士によって提唱された概念です。このスキルミオンと同等な状態が、液晶や磁性体といったさまざまな物質中でも観測できることが最近発見され、特に磁性体中のスキルミオンは、渦巻き状のスピン構造として発現することが知られています。
- 注2)スピン
- エレクトロニクスの主役である電子は、電荷とスピンの2つの自由度を持つ粒子であることが知られており、後者のスピンの自由度は、電子の自転が生み出す角運動量に由来しています。スピンは極めて小さなサイズの棒磁石のような性質をもっており、磁性体の中ではこのスピンが一定の規則に従って整列した状態が実現しています。従来の半導体素子では、主に電荷の流れである電流が用いられて来ましたが、このアプローチではジュール発熱(電流の2乗に比例)によるエネルギー損失が必ず生じるという課題があります。一方、スピンの流れであるスピン流は本質的にエネルギー非散逸であることから、スピンの自由度を活用することで、情報処理にまつわる消費電力を劇的に削減できることが期待されています。
- 注3)トポロジー
- トポロジーとは、連続変形を行っても保たれるような何らかの不変量によって、物体の「形」を分類する考え方のことを指します。例えば、物体に空いた穴の数や、ひもの結び目の数といったものがこの不変量に相当しており、こうした穴や結び目は連続変形では取り除けないことから、特別な安定性を持つことが知られています。