AIに電子の物理を学習させる方法を開発
東京大学
発表のポイント
- AIなどに使われている機械学習手法を物理理論と組み合わせることで、電子状態の予測精度を向上する方法を開発した。
- 分子内の電子のとる状態を機械学習させ、電子間の相互作用を抽出し、それを理論に取り入れることで幅広い物質に対して高精度に電子状態を計算できることを示した。
- 開発された技術をさらに精巧化することで、物性の解明や、未知の物質の設計・探索などがより確実に行えるようになると期待される。
発表概要:
東京大学大学院理学系研究科物理学専攻の永井瞭大学院生、明石遼介助教、同大学物性研究所の杉野修教授らの研究グループは、AI技術などに使われる機械学習手法(注1)を応用し、物質の電子状態を計算する密度汎関数理論(DFT、注2)における不完全な項を補完する方法を開発しました。小分子における高精度計算の結果を参照し、機械学習モデルにDFTにおける電子間相互作用の記述方法を学習させ、その項を用いたDFT計算をさまざまな分子に適用し精度検証しました。結果、これまで60年以上の研究で開発されてきた計算方法と同等かそれ以上の精度を示すことがわかりました。
物質のもつ性質の多くは電子によって支配されており、電子状態の理論的解明は物性の理解や高機能物質の探索・設計などにおいて重要な課題です。現在電子状態の計算には、計算コストの小ささからDFTという理論に基づく手法が主に使われています。しかし、この理論の中には電子間の相互作用について厳密に記述できない項が現れます。実用計算ではこの項は何らかの方法で近似されるのですが、これまで開発されてきた近似では単純すぎて、本来複雑であるはずの電子間相互作用を記述しきれておらず、計算精度に問題が生じうることが知られています。
今回の成果により、計算に電子間相互作用を精密に取り入れることが可能になりました。また本成果では記述・精度向上をさらに進める系統的方法も提示しており、今後さらなる電子状態の予測性能向上が期待されます。
本成果は英国科学雑誌npj Computational Materialsに2020年5月5日付けオンライン版に公開されました。
発表内容:
①研究の背景
金属や半導体を用いた電子機器や、高度な機能を持つ分子を利用した薬品など、我々の生活はさまざまな物質によって支えられています。これらの物質のもつ性質の起源には、電子が重要な役割を果たしているため、電子のふるまいを理解することが物質の研究・開発には欠かせません。電子のふるまいを理論的に説明するために、基本的な物理法則である量子力学に基づいた第一原理計(注3)によるシミュレーションが盛んに行われています。しかし、量子力学の基礎方程式であるSchrödinger方程式(注4)では電子の多体相互作用を扱うため、解くのに必要な計算コストが電子数に対して指数関数的に増大します。現代の計算機では限られた大きさの系しか扱うことができずSchrödinger方程式を直接扱うのは実用的ではありません。一方、DFTによると、Schrödinger方程式から得られる基底状態の物理量の一部は、相互作用のない形の方程式(Kohn-Sham方程式)を解くことでも計算可能です。Kohn-Sham方程式はその計算量の手軽さから数多くの物質の電子状態解明に用いられ、第一原理計算のスタンダードとなりました。
しかし、計算コストを圧縮した代償としてKohn-Sham方程式には電子間相互作用について厳密に書き下せない項(交換相関汎関数、または単に汎関数と呼ぶ)が現れます。これまでのKohn-Sham方程式の応用計算ではこの項についてさまざまな近似形が提案されてきました。実際の計算精度はこの近似が対象の物質中の電子のふるまいをよく記述しているかどうかで決まります。しかし、これまで開発されてきた近似汎関数は解析的に構築しやすい単純な関数形をしており、本来非常に複雑であるはずの電子間相互作用を記述しきれていないという問題があります。結果として、すべての物質の電子状態を包括的に精度良く扱うことはできず、近似法によって得意な物質と苦手な物質が存在してしまう、という状況になっています。これでは、たとえば未だ物性が調べられていない新物質の計算において、信頼して用いることができません。また、どのような近似方法を用いても精度良く記述できない物質も知られています。
従来、汎関数の構築は、理想的な汎関数が満たすべき漸近形や不等式などを調べ、それらの条件を満たすような関数形を場合に応じて構成し用いられてきました。しかし、どの条件をどのように組み合わせるかには恣意性が含まれてしまいます。これまでの汎関数開発では、さまざまな組み合わせ方で作られた汎関数をさまざまな物質に適用してみて、結果として一番性能が良かったものを皆で利用する、という発見的な方法に基づいていました。このような発見的な手順では、汎関数の近似法の改善のために、系統的な道筋が明らかではないという問題があります。
②研究内容
電子相互作用を高精度に再現させるため、Schrödinger方程式に基づいて精度良く解かれた、いくつかの小分子の電子状態データを用意し、機械学習の訓練データとしました。そして、Kohn-Sham方程式に含まれる汎関数項に機械学習モデルであるNeural Network(NN、注5)を電子間の相互作用モデルとして埋め込み、訓練データ内の電子のふるまいを再現するようにNNの訓練(内部パラメータの最適化)を行いました(図1)。訓練済みのNNを用いたKohn-Sham方程式を、訓練データに含まれない数百の小〜中分子系に適用し解離エネルギーなどの計算精度を検証したところ、その精度が既存の汎関数と同等以上であることが判明しました。
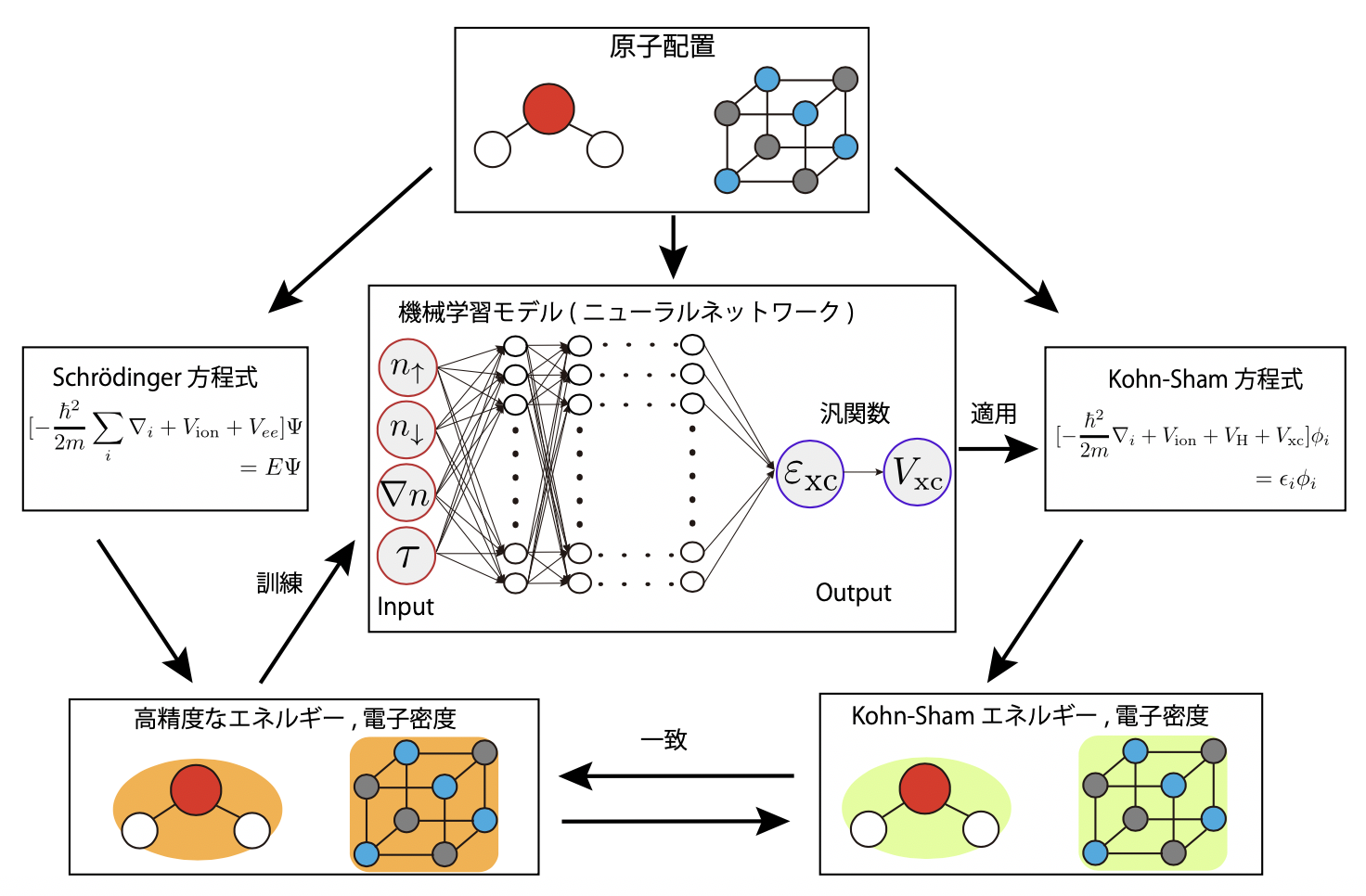
さらに、従来の汎関数の近似精度を系統的に超えていく方法を提示しました。これまでの近似では、ある地点の電子が、ごく近傍の電子のみと相互作用するような単純な近似法が取られていました。これは、そのような単純な形式でないと参照すべき条件を代数的に計算できなかったためです。一方、機械学習を用いた本手法ではデータを用いて汎関数形が決定できるため、より遠方の電子と相互作用するようなモデルも、データのみから最適なものを構築することができます。発表者らはこの利点を活かし、実際に機械学習手法を用いて遠距離相互作用を取り入れる複雑な構造をもつ汎関数を構築し、性能を検証しました。その結果、従来の近似よりも改善が得られることが示されました(表1)。
| 汎関数名 | 原子化エネルギーの平均誤差 AE147 (kcal/mol) |
|---|---|
| M06-L | 5.2 |
| NN-metaGGA(本成果) | 4.7 |
| B3LYP | 4.5 |
| NN-NRA(本成果) | 3.7 |
③社会的意義・今後の展望
今回の研究を通して、機械学習を用いて汎関数を構築する道筋が確立され、また既に分子系に対しては既存の汎関数以上の精度を持つ汎関数が得られました。今回提案した方法をさらに推し進め、大量のデータを用いて訓練することで、従来の電子状態計算では到達し得なかった汎用性と精度を備えた汎関数の構築が期待できます。特に、従来は分子・固体など系により最適な汎関数が異なっていたのに対し、汎関数の複雑さを上げることでその両方を記述できる可能性があります。汎用性を高めてゆくことができれば、あらゆる物質に対して信頼して用いることができる電子状態計算手法が確立されることとなり、未知の物質の探索・設計においてより確実に物性の予測が行えることが期待されます。
発表雑誌:
- 雑誌名:npj Computational Materials
- 論文タイトル:Completing density functional theory by machine learning hidden messages from molecules
- 著者:Ryo Nagai*, Ryosuke Akashi, Osamu Sugino
- DOI番号:10.1038/s41524-020-0310-0
用語解説:
- (注1) 機械学習(教師あり学習)
- ある2つのデータの間の関係・写像・関数を、多量のパラメータを持った機械学習モデルで数値的に模倣する方法。データの組み合わせをいくつか予めサンプリングしておき、その組み合わせを再現するように機械学習モデルを訓練させ、訓練された機械学習モデルを未知のデータに適用することで予測を行う、という一連の流れを指す。たとえば、画像認識問題における「ある画像のピクセルデータ」→「その画像が何を表しているかのラベルor言語データ」の関係など、人間の手では複雑すぎて数理的なモデルが建てられないような関係に対して適用される。特に、機械学習により人間の知覚・行動を模倣させることをAIと呼ぶ。
- (注2)密度汎関数理論(Density functional theory, DFT)
- 量子多体問題を記述する基礎方程式であるSchrödinger方程式では粒子間の相互作用部分が粒子数に対して指数関数的な大きさの変数空間を持つ波動関数を扱わなければならず、計算コストが実用的ではない。そこで開発されたのがDFTであり、この理論では、波動関数の代わりに電子密度を取り扱っても、もとのSchrödinger方程式とおなじ基底状態が解となる変分問題が存在することを示している。電子密度は変数空間の大きさが粒子数によらず、このDFTの変分問題を実際に実行可能とするKohn-Sham法では相互作用のない仮想的な方程式を解けばよい。そのため、Schrödinger方程式よりも遥かに手頃な計算コストで電子状態を求めることができる。ただし、理論中に電子密度では解析的に書き下せない項が現れる(交換相関汎関数)。
- (注3)第一原理計算
- 原子核や電子の配置など、物質を構成する基本的な構成要素のみをインプットとし、量子力学に基づきその性質をシミュレーションする方法。実験では観測できない微視的な情報を得られるため、物性の理解に重要な役割を果たす。また、未知の新物質に対して物性を予測することで、高機能な物質や学問的に興味深い性質をもった物質の探索・設計に応用することができる。
- (注4)Schrödinger方程式
- 電子などの軽い粒子の従う物理法則である量子力学における基礎方程式。Schrödinger方程式を解く計算コストは粒子数の数に対して指数関数的に増大するため、直接適用できる範囲は最大でも10原子程度である。
- (注5)Neural Network(NN, ニューラルネットワーク)
- 機械学習モデルのひとつ。線形変換と非線形変換を多重に施すことで複雑性をもたせたモデルである。十分な大きさを持ったNNは任意の関数を任意の精度で近似できることが示されている。また、大規模なNNを用いて機械学習を行なうことをディープラーニングと呼び、近年の応用分野では注目の的となっている。
