The concept of a quasiparticle has been successful in explaining various types of low-energy excitations in many-body systems including charge, spin, and lattice. Using a spectroscopic approach, a weakly coupled quasiparticle with a long lifetime can be probed as a well-defined excitation, allowing identification of the effective Hamiltonian and basic understanding of the system. Momentum-resolved spectroscopy has permitted investigations into the intricate structure of spectra, revealing the effect of quasiparticle interactions that results in the renormalization of the dispersion and instability of the quasiparticle.

The microscopic phenomena in the spectra affect bulk properties of materials. In the thermoelectric material PbTe, the interaction between longitudinal acoustic and transverse optical modes (here, the quasiparticles are phonons) induces the decay and overdamping of the former phonon in the low energy region, leading to low conductivity of thermal current [1]. The instability of the quasiparticle is key for the current to exist in bulk property.

Two examples illustrate that the instability of the quasiparticle is changed by the interaction between the one-quasiparticle and two-quasiparticle continuum [2]. An example for a case of the strong interaction is found in the longitudinal sound wave, phonon, in superfluid ⁴He [3]. The spectrum in low energy exhibits a local minimum with energy Δ, called a roton, for which qualitative behavior is explained by Feynman and Cohen (FC) harmonic dispersion. However, the spectrum does not exceed a critical energy of 2Δ, which is the lower boundary of the two-phonon continuum. The strong interaction between the one-phonon and continuum pushes one-phonon energy downwards, and the one-phonon stays at 2Δ outside the continuum. On the FC dispersion beyond the critical energy, the bare one-phonon decays into a pair of rotons, and a remnant of one-phonon which is ascribed to the bound state of two-phonon was observed. The phenomenon is considered universal in bosonic systems and has also been observed in a spin-gap antiferromagnet BiCu₂PO₆ [4].

An example for the weak interaction is found in a two-dimensional quantum magnet, piperazinium hexachlorodicuprate (PHCC) [3]. This case is simple; the quasiparticle decays in the continuum, and a remnant one-magnon is probed as a broad excitation. The conjecture which this work tests is that if one tunes the interaction between a quasiparticle and the continuum in an identical material by applying external field, would the quasiparticle decay behavior change?

This study [5] examines magnon decay in a triangular lattice quantum antiferromagnet RbFeCl₃. Magnetism of Fe²⁺ ion surrounded by Cl- octahedra with trigonal distortion is effectively described by an S = 1 spin with strong easy-plane anisotropy. Fe²⁺ ions form a one-dimensional ferromagnetic chain along the crystallographic c-axis, and the interchain interaction in the triangular lattice in the ab-plane is antiferromagnetic. At low temperatures the compound exhibits a non-collinear 120° structure due to the frustration. The spectrum was qualitatively similar to that of the pressure-induced ordered state in the isostructural compound CsFeCl₃ near the quantum critical point (QCP) [6], which cannot be explained by standard linear spin wave theory. Instead, the strong hybridization of the transverse and longitudinal fluctuations resulting from the non-collinear magnetic structure renormalizes the magnetic excitation, as explained by the linear extended spin wave theory (LESW) [3]. Because a non-colinear magnetic structure is realized near the QCP and the excitation is strongly hybridized with longitudinal fluctuation, the magnon decay is anticipated in wide four-dimensional momentum-energy space. Furthermore, gapless behavior and a large dispersion perpendicular to the triangular lattice yield a two-magnon continuum covering the whole region of one-magnon excitation.

In this study, we performed inelastic neutron scattering (INS) measurements in the magnetic field on RbFeCl₃ to study the magnon decay and the interaction between single magnons and the two-magnon continuum. We observed a simple magnon decay in a low field where the interaction is small and a magnon avoiding decay in high field where the interaction was large as shown in Fig. 1. Thus, we succeeded in controlling the magnon decay using the field. In contrast with the avoided phonon decay in superfluid ⁴He and magnons in magnetic materials previously reported [2,4], the phenomenon was observed in the presence of a two-quasiparticle continuum, indicating that the phenomenon is not limited to outside the continuum, but also occurs inside.

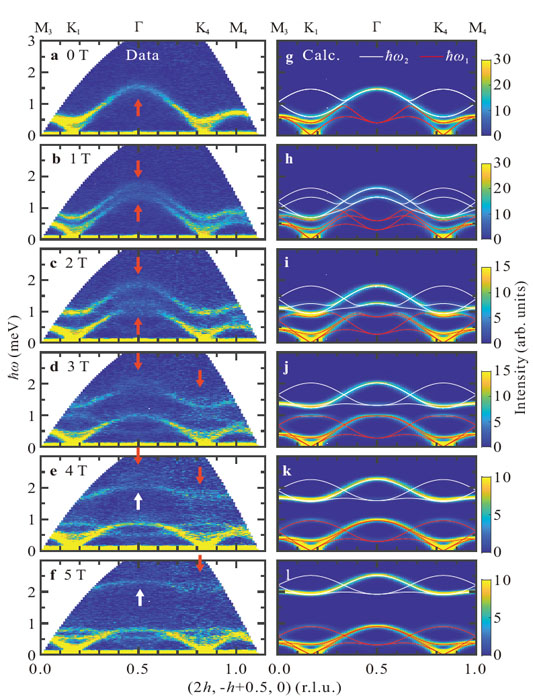
Fig. 1. False color map of inelastic neutron scattering (INS) spectra and calculated two-magnon density of state in RbFeCl₃. a-l: Magnetic field (H // c-axis) dependences of false color maps for observed (a-f) and calculated (g-l) INS spectra. Red arrows in a-f indicate broadening linewidth. White arrows in e and f indicate magnons avoiding decay. White and red solid curves in g-l are one-magnon dispersion relations of ħω₁ and ħω₂ modes calculated using linear extended spin wave theory (LESW) using the best fit parameters. The calculated spectra are convoluted by the instrumental resolution.

References

• [1] O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M. H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden, and B. C. Sales, Nat. Mater. 10, 614 (2011).
• [2] R. Verresen, R. Moessner, and F. Pollmann, Nat. Phys. 15, 750 (2019).
• [3] M. B. Stone, I. A. Zaliznyak, T. Hong, C.L. Broholm, and D. H. Reich, Nature (London) 440, 187 (2006).
• [4] K. W. Plumb, K. Hwang, Y. Qiu, L. W. Harriger, G. E. Granroth, A. I. Kolesnikov, G. J. Shu, F. C. Chou, C. Rüegg, Y. B. Kim, and Y-J. Kim, Nat. Phys. 12, 224 (2016).
• [5] S. Hasegawa, H. Kikuchi, S. Asai, Z. Wei, B. Winn, G. Sala, S. Itoh, and T. Masuda, Nat Commun 15, 125 (2024).
• [6] S. Hayashida, M. Matsumoto, M. Hagihala, N. Kurita, H. Tanaka, S. Itoh, T. Hong, M. Soda, Y. Uwatoko, and T. Masuda, Sci. Adv. 5, eaaw5639 (2019).

Authors

• S. Hasegawa, H. Kikuchi, S. Asai, Z. Wei, B. Winn^a, G. Sala^a, S. Itoh^b, and T. Masuda,
• ^aOak Ridge National Laboratory
• ^bKEK