Shear-Strain Controlled High-Harmonic Generation in Graphene
Kato and Akiyama Groups
Two-dimensional (2D) Dirac electrons in single-layer graphene have attracted much attention for their novel linear and nonlinear optical properties. One-atom-thick graphene exhibits universal frequency-independent light absorption, πα = 2.3%, where α = e2/ħc ≈ 1/137 is the fine structure constant [1]. Ultrafast carrier dynamics on massless bands provide a variety of high-speed broadband optical responses. Further studies have targeted artificial control, modulation, or switching of these properties for potential applications in graphene-based optical devices. However, the robustness of optical transition probability πα inherent to 2D Dirac electrons makes the external control of optical responses highly challenging.
A graphene sheet has high flexibility and a shear strain of up to 27% can be reversibly applied to it [2]. This strain effect should be useful for control of the nonlinear optical responses of graphene. In this study [3], we theoretically demonstrated a significant enhancement or quenching of HHG over several orders of magnitude in graphene by tuning the shear strain and the incident-light polarization angle (Fig. 1 (a)).
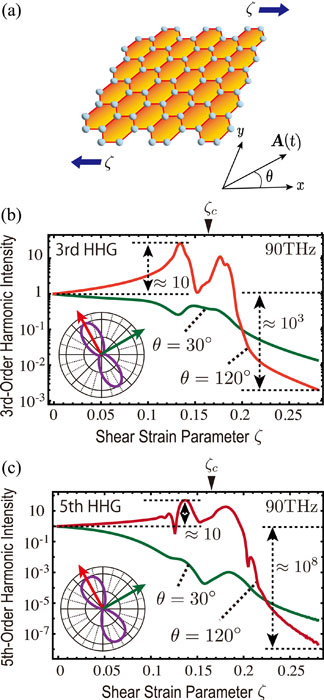
Fig. 1. (a) Schematic figure of lattice structure of graphene under shear strain. The amplitude of the shear strain is represented by ζ and the vector potential of the incident light is denoted as A(t), whose tilt angle measured from the armchair axis is described by θ (see the inset). (b) Shear strain dependence of the third- and fifth-order harmonics. The red and green lines indicate the high-harmonic intensities for the incident-light angles θ = 120˚ and θ = 30˚, respectively. The polarization angle dependences of the third and fifth harmonics for ζ = 0.12 are shown in the insets. The critical strength of the shear strain for a band gap to form is described by ζc.
We show the shear-strain dependences of the third and fifth harmonics in Fig. 1 (b) and (c). The red and green lines indicate the dependences for the different incident-light polarization angles, θ = 120˚ and θ = 30˚, respectively (for definition of theta, see Fig. 1 (a)). These two angles are regarded as the specific ones because they can yield the maximum and minimum intensities of the emitted harmonics (see insets in Fig. 1 (b) and (c)). Fig. 1 (b) and (c) show that, for θ = 120˚, the third-order (fifth-order) harmonics are largely enhanced by around one order of magnitude at ζ ≈ 0.13 and 0.18, while they are quenched rapidly by around third (eight) orders of magnitude at 0.2 < ζ < 0.27 (red line), where ζ is the amplitude of the shear strain. The plots for θ = 30˚ do not show this nonmonotonic behaviour; they only show an approximately monotonic decrease with increasing shear strain. By using linear response theory, we showed that the HHG enhancement came from the resonances at which the incident-light photon energy matches the saddle-point energy or the band gap [3]. In addition, the dipole moment near the saddle point (or the band gap) plays an important role in the polarization angle dependence of this enhancement. Strong quenching of HHG was induced by rapid growth of the band-gap energy with increasing shear strain.
In conclusion, we theoretically investigated the linear and nonlinear optical responses of graphene distorted by shear strain. Using the tight-binding model, we clarified that tuning both the shear strain and the polarization angle of the incident THz light enables a significant enhancement or quenching of HHG. Our findings suggest the possibility of using shear strain to control HHG in graphene and pave the way for optical nanotechnology of single-layer materials.
References
- [1] R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. Peres, and A. K. Geim, Science 320, 1308 (2008).
- [2] Z. Peng, X. Chen, Y. Fan, D. J. Srolovitz, and D. Lei, Light: Sci. Appl. 9, 190 (2020).
- [3] T. Tamaya, H. Akiyama, and T. Kato, Phys. Rev. B 107, L081405 (2023).
