Recently, a novel type of magnetoresistance, called spin Hall magnetoresistance (SMR), has been attracting much attention. SMR was first observed in a normal metal (NM)/ferromagnetic insulator bilayer [1] and subsequently in a NM/antiferromagnetic insulator (AFI) bilayer [2]. Because SMR reflects information on the FI magnetization or AFI Néel vector, it can be utilized for detecting the orientation of ordered spins in magnetic materials. Although the existing theory [1,3] succeeds in explaining the qualitative features of SMR measurements, it could not explain the temperature dependence of the SMR signal. Recently, a microscopic theory using Green's function has been constructed [4]. This microscopic theory describes SMR in terms of local spin susceptibilities of the FI(AFI). It can include dynamic processes such as magnon absorption and emission responsible for a nontrivial sign change in the SMR signal, which are neglected in the semiclassical theory.

In this study, we numerically calculated SMR by using a quantum Monte Carlo method [5] for a NM/AFI bilayer (see Fig. 1 (a)). We utilized an improved method for accurately obtaining the integral of the local spin susceptibilities from the QMC data without using numerical analytic continuation. We evaluated the detailed temperature dependence of SMR for S = 1/2 and S = 1 spin systems on a two-dimensional square lattice and a quasi-two-dimensional cubic lattice with a finite number of layers.

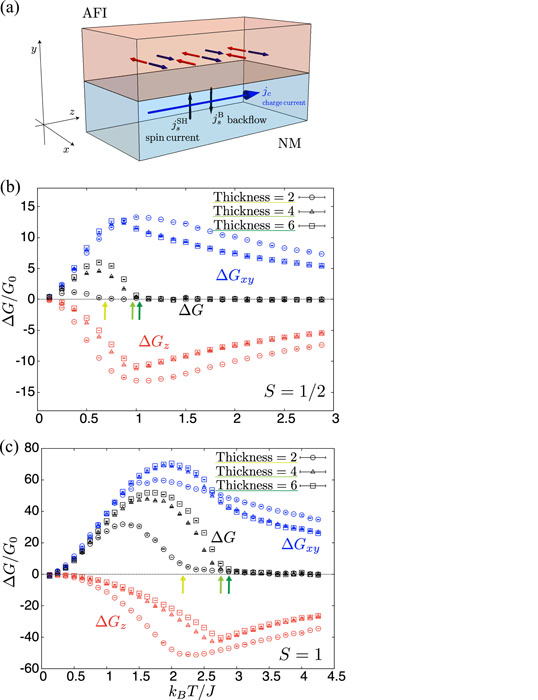
Fig. 1. (a) Illustration of spin Hall magnetoresistance. Spin absorption at the interface changes according to the orientation of the Néel vector of the antiferromagnetic insulator, and the magnitude of the magnetoresistance changes. (b,c) Temperature dependences of spin conductance ΔG are shown for (b) S = 1/2 and (c) S = 1 quantum Heisenberg model. The two contributions, ΔG_xy and ΔG_z, are plotted separately.

Figure 1 (b) shows the spin conductance, which is proportional to the SMR signal, for the S = 1/2 quasi-two-dimensional quantum Heisenberg model on a 16 × 16 × W (W = 2, 4, 6) cubic lattice. As the thickness W increases, the ordering temperature (indicated by the green arrows) increases. The spin conductance induced below the transition temperature becomes large while it vanishes above the transition temperature. We find that the peak of the spin conductance is greatly enhanced compared with that for a single-layer spin system (not shown). Although the maximum of the spin conductance increases with increasing thickness W, the difference between the results for W = 4 and 6 is much smaller than that for W = 2 and 4. Figure 1 (c) shows the SMR signal for the S = 1 quasi-two-dimensional quantum Heisenberg model on a 16 × 16 × W (W = 2, 4, 6) cubic lattice. As the thickness W increases, the ordering temperature (indicated by the green arrows) raises and the SMR signal becomes large. Above the transition temperature, the SMR signal becomes small but remains finite, in contrast with the case of S = 1/2. We showed that this feature can be understood well by the high-temperature expansion. As the temperature decreases below the ordering temperature, the SMR signal increases, takes a maximum roughly at three-fifths of the ordering temperature, and then decreases. The maximum value of the signal is rather larger than in the case of S = 1/2. At sufficiently low temperatures, the SMR signal becomes negative, as predicted by the spin-wave approximation. We also discussed the effect of the disordered exchange interactions.

In our study, we succeeded in clarifying the qualitative features of SMR based on the numerical results. These qualitative features are expected to be observed experimentally. Our simulation using a simplified model is expected to be a useful starting point for understanding SMR in quasi-two-dimensional quantum spin systems.

References

• [1] H. Nakayama et al., Phys. Rev. Lett. 110, 206601 (2013).
• [2] D. Hou et al., Phys. Rev. Lett. 118, 147202 (2017).
• [3] Y. T. Chen et al., Phys. Rev. B 87, 144411 (2013).
• [4] T. Kato, Y. Ohnuma, and M. Matsuo, Phys. Rev. B 102, 094437 (2020).
• [5] T. Ishikawa, M. Matsuo, and T. Kato, Phys. Rev. B 107, 054426 (2023).

Authors

• T. Ishikawa, M. Matsuo, and T. Kato