Weyl magnets, which have the topologically nontrivial band crossing points, have recently attracted significant attention because of the unconventional physical properties, such as large anomalous Hall effects (AHE). The typical materials have a semimetallic band structure where many bands cross the Fermi energy (E_F), resulting in complicated band structures and Fermi surfaces that hinder a simple understanding of their Weyl physics. In this study, we report on the field-tunable Weyl points in the degenerate antiferromagnetic semiconductor EuMg₂Bi₂, which has a simple and small Fermi surface. EuMg₂Bi₂ has a CaAl₂Si₂-type structure, which consists of the alternative stacking of the Eu magnetic layer and the Mg₂Bi₂ buckled-honeycomb layer (Fig. 1(a)). The former layer exhibits the A-type antiferromagnetic (A-AFM) order below T_N ~ 6.7 K at zero field. When the field is applied along the c -axis, Eu spins start canting toward the c-axis and are fully polarized above B_c ~ 4 T at 2 K. The latter layer forms the semiconducting band with the direct band gap at the Γ point, resulting in the simple Fermi surface. Therefore, it is expected that, in the magnetic field, the spin-polarized band crossing points (Weyl points) are formed while maintaining a simple band structure due to the spin splitting caused by the exchange interaction with local Eu spins. To reveal the impacts of the Eu magnetism on the band structure of EuMg₂Bi₂, we synthesized the large single crystal (Fig. 1(b)) and performed the various measurements and the first-principles calculations.

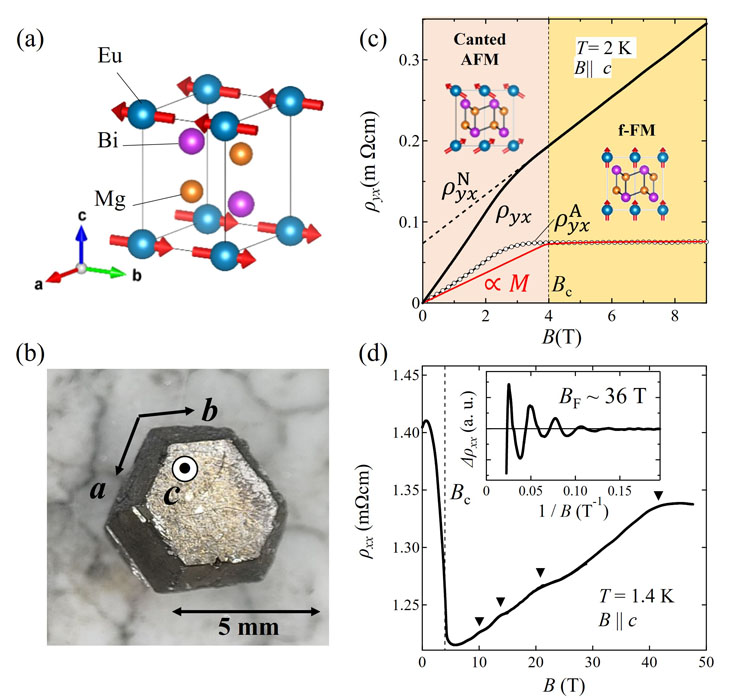
Fig. 1. (a) The crystal structure of EuMg₂Bi₂. (b) The photograph of the single crystal of EuMg₂Bi₂. (c) The field dependence of ρ_yx and its anomalous part ρ^A_yx at 2 K. The black dotted line corresponds to the ordinary part ρ^N_yx obtained from the liner fit to the experimental data above B_c. Note here that the ρ^N_yx is vertically shifted to demonstrate the fitted result at the high-field region. The red curve represents the field dependence of the magnetization M at 2 K. Insets show the magnetic structure of Eu spins at canted-antiferromagnetic (AFM) and forced-ferromagnetic (f-FM) phases. (d) Field dependence of ρ_xx at T = 1.4 K up to B ~ 50 T. Triangles denote the oscillatory component. The inset shows the oscillatory component Δρ_xx.

Figure 1(c) shows the field dependence of the Hall resistivity ρ_yx at 2 K for the field along the c-axis. Although, ρ_yx is almost linear with respect to field above B_c, it deviates from the straight line below B_c and shows a hump structure at approximately 2.5 T. This signals the AHE coupled with Eu magnetic order. To extract the anomalous component ρ^A_yx, we estimate the ordinary component ρ^N_yx  = R_HB from the data abobe B_c. We obtained the anomalous conponent as ρ^A_yx = ρ_yx - ρ^N_yx which is roughly proportional to magnetization. At B > B_c, the anomalous Hall angle Θ_AH = σ^A_xy / σ_xx, where σ^A_xy = ρ^A_yx / (ρ²_xx + ρ²_yx) and σ_xx = ρ_xx / (ρ²_xx+ρ²_yx) exhibits the nearly constant value (~ 0.07), which is comparable to those reported for other Weyl ferromagnets Co₃Sn₂S₂ (~ 0.2 at 150 K) [2], Fe₃GeTe₂ (~ 0.09 at 2 K) [3], and GdPtBi (~ 0.15 at 2.5 K) [4]. Such a large Θ_AH indicates that EuMg₂Bi₂ has band crossing points near E_F in the forced-ferromagnetic (f-FM) phase as a source of the Berry curvature.

To obtain the detailed information of the Fermi surface, we measured the several physical properties up to ~ 55 T using the nondestructive mid-pulse magnet. Figure 1(d) shows the field dependence of the resistivity ρ_xx. As denoted by black triangles, we observed clear oscillatory structure. These oscillations are periodic with respect to 1/B [see inset of Fig. 1(d)], which indicates the quantum oscillation arising from the Landau quantization. By Onsager’s theorem, we can estimate the cross-section S_F (~ 0.352 nm^-2) of the Fermi surface from the oscillation frequency B_F (~ 36 T), which allows us to determine the position of E_F in combination with the first-principles calculation shown below.

Figure 2(a) shows the calculated band structure around the Γ point for A-AFM phase. The two valence bands I and II cross each other on the Γ−A line, leading to a Dirac-like point located far from the E_F. When the field is applied along the c-axis, both bands exhibit a spin splitting because of the exchange interaction with the local Eu spins to form the multiple Weyl points. The position of the Weyl points shifts with increasing the magnitude of the spin splitting. Intriguingly, in the f-FM phase, one of the Weyl points are formed in the vicinity of E_F (Fig. 2(b)), which is determined to be ~ 110 meV from the comparison between the experimental and theoretical values of S_F and carrier density obtained from the Hall coefficient [1]. To clarify the intrinsic AHE due to the Berry curvature of the Weyl point, we calculated the E_F dependence of the anomalous Hall conductivity σ^A_xy in the f-FM phase. The calculated σ^A_xy shows a peak near the experimental E_F value where the Weyl point exists, and a good quantitative agreement with the experimental result obtained by the carrier-tuned samples. This strongly indicates that the observed large AHE in EuMg₂Bi₂ is due to the Berry curvature at the Weyl point induced by the magnetic field. Thus, our findings have clarified the unambiguous relationship between the emergent Weyl points and the anomalous Hall effect in a simple band structure, providing a guiding principle for future material design.

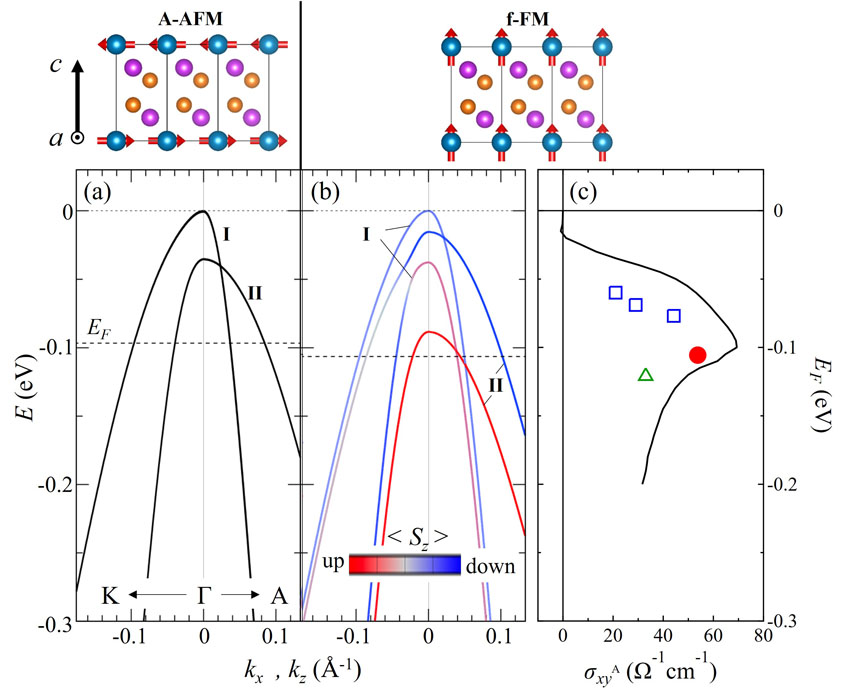
Fig. 2. (a, b) Valence band structures around the Γ point near E_F (lower panels) for various magnetic states (upper panels). Red and blue colors of band dispersions represent spin up and spin down, respectively. The dotted lines denote the Fermi energy E_F determined from the quantum oscillation frequency B_F at T = 1.4 K. (c) Anomalous Hall conductivity σ^A_xy as a function of E_F. The solid black curve represents the calculated result for the f-FM phase. The solid red circle denotes the experimental data (2 K, 9 T) for pristine EuMg₂Bi₂, while the open blue squares and open green triangle denote those for the annealed crystals and In-doped crystal, respectively.

References

• [1] M. Kondo et al., Physical Review B 107, L121112 (2023).
• [2] E. Liu et al., Nat. Phys. 14, 1125 (2018).
• [3] K. Kim et al., Nat. Mater. 17, 794 (2018).
• [4] T. Suzuki et al., Nat. Phys. 12, 1119 (2016).

Authors

• M. Kondo^a, M. Ochi^a, R. Kurihara^b, A. Miyake, Y. Yamasaki^c,d, M. Tokunaga, H. Nakao^e, K. Kuroki^a, T. Kida^f, M. Hagiwara^f, H. Murakawa^a, N. Hanasaki^a, and H. Sakai^a
• ^aOsaka University
• ^bTokyo University of Science
• ^cNIMS
• ^dCEMS, RIKEN
• ^eKEK
• ^fAHMF, Osaka University