Yb–T–X (T: transition metal, X: pnictogen) ternary compounds have been studied intensively in terms of novel phenomena in the vicinity of the magnetic quantum critical point (QCP). For example, YbNi₄P₂ is reported to be close to the ferromagnetic QCP, exhibiting the ferromagnetic transition (FM) at 0.17 K [1]. The field-induced non-Fermi liquid behavior of Yb₂Fe₁₂P₇ has also attracted attention [2].

To our knowledge, no ternary compound of Yb–Ru–As has been reported. In this study, we have investigated ternary Yb–Ru–As compounds and found a compound Yb₄Ru₇As₆, which crystallizes in the U₄Re₇Si₆-type cubic structure, showing a weak ferromagnetic (FM) behavior below T₀~4.0 K and antiferromagnetic (AFM) ordering at T_N = 2.5 K with the moderately enhanced electronic specific heat coefficient of 120 Yb-mJ/K²mol [3].

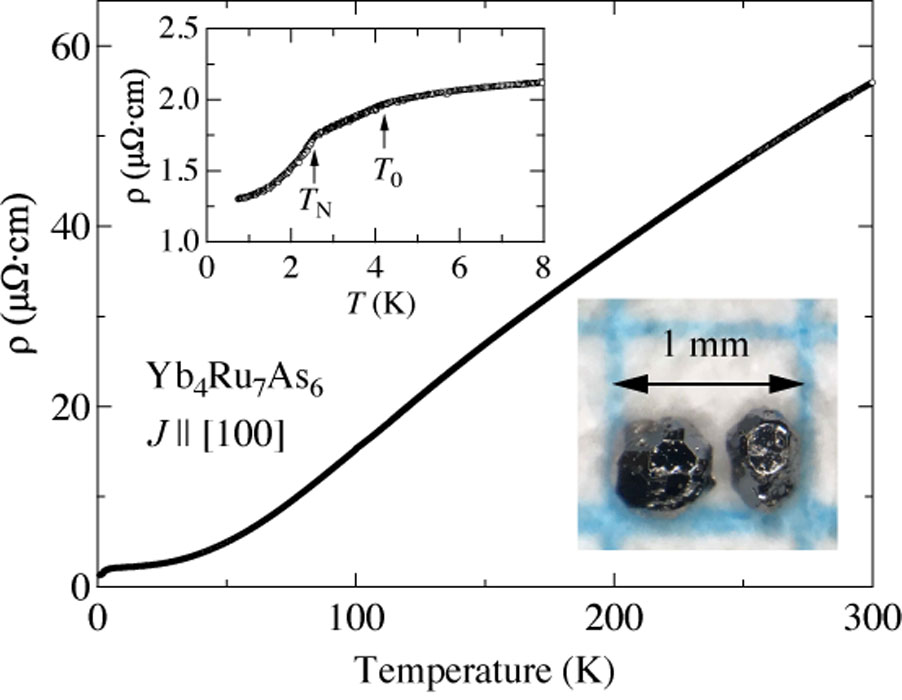
Single crystals of Yb₄Ru₇As₆ were grown by the Bi-flux method, and obtained crystals are shown in the inset of Fig. 1. The crystal structure of Yb₄Ru₇As₆ is determined to be the cubic U₄Re₇Si₆-type structure (No.229, Im3m) using a XtaLAB HyPix-600HE diffractometer. Note that the local symmetry of Yb atom is similar to rare earth metals in skutterudite. Fig. 1 shows the temperature dependence of the electrical resistivity ρ of Yb₄Ru₇As₆ for the current J along the [100] direction. With decreasing temperature, ρ monotonically decreases with a shoulder-like structure below 10 K. At low temperatures, two inflection points at T₀~4 K and T_N~2.5 K in ρ are observed, as shown in the inset of Fig. 1. The residual resistivity ratio is about 40, indicating a high-quality sample.

Fig. 1. Temperature dependence of ρ of Yb₄Ru₇As₆. The magnification of the low temperature part and photograph of single crystals are shown in inset.

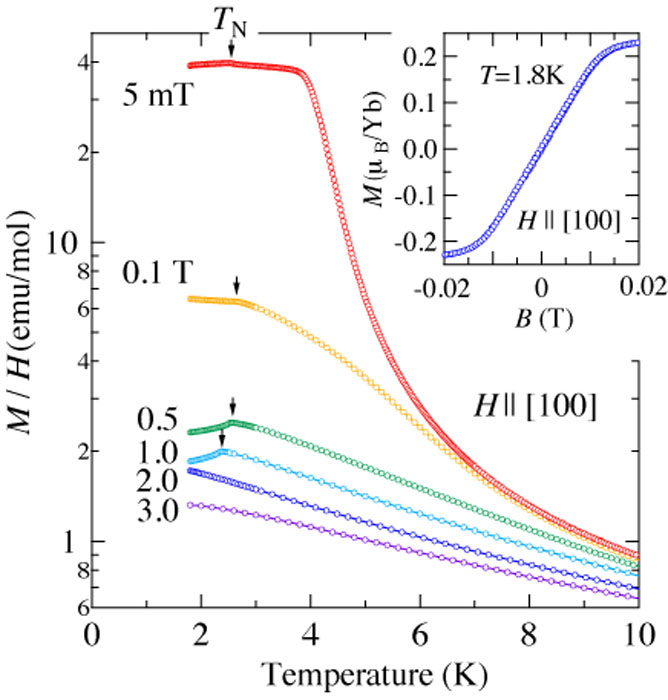
Magnetic properties are isotropic reflecting the cubic structure. With decreasing temperature, magnetic susceptibility M/H increases and follows the Curie–Weiss law at temperatures higher than 150 K. The estimated effective magnetic moments are 4.28–4.45 μB/Yb, which is close to the expected value of Yb³⁺ ionic state: 4.54 μB/Yb. Fig. 2 shows the temperature dependences of M/H for H || [100] below 10 K measured at several magnetic fields. M/H at 5 mT shows a ferromagnetic increment in the temperature range between 6 and 4 K, and a small peak at 2.5 K. Note that no detectable hysteresis loop is observed in magnetization at 1.8 K, as shown in the inset of Fig. 2. With increasing temperature, the peak temperature decreases to 2.25 K at 1.0 T and disappears above 2.0 T, meaning that the peak in M/H corresponds to the AFM transition.

Fig. 2. M/H for H || [100] below 10 K at several magnetic fields. Inset shows the magnetization curve for H || [100] at 1.8 K in low magnetic fields.

The specific heat C shows an upturn below 7.5 K and λ type sharp peak at 2.5 K, corresponding to the short-range magnetic correlation and/or the Kondo effect, and the long-range magnetic ordering, respectively. In addition, a tiny anomalous behavior is observed at T₀~4 K, which corresponds to the temperature where the anomaly in ρ and the occurrence of the FM behavior emerge as mentioned above. It means that T₀ can be attributed to a temperature characterizing the FM behavior. T_N is shifted to lower temperatures under magnetic fields and seems to disappear at 2.5 T. On the other hand, the tiny anomaly at T₀ becomes obscure in the magnetic fields.

The characteristic temperature where the FM behavior in M/H is observed corresponds to the beginning of the short-range ordering as observed in the temperature dependence of C, implying that one of the possibilities of the FM in Yb₄Ru₇As₆ is considered a concomitant phenomenon of the AFM ordering with a canted magnetic moment arrangement from the <100> direction. The canted AFM can be realized in the condition of magnetic interaction and magnetocrystalline anisotropy favoring the non-antiparallel arrangement of magnetic moments. Since there is no inversion symmetry at the center between the nearest neighbor magnetic Yb sites, the Dzyaloshinskii–Moriya interaction can be one of the possible origins of FM behavior, for example. To elucidate the origin of T₀, resistivity measurements in magnetic fields are in progress, and further experiments with microscopic probes are needed.

References

• [1] C. Krellner, S. Lausberg, A. Steppke, M. Brando, L. Pedrero, H. Pfau, S. Tencé, H. Rosner, F. Steglich, and C. Geibel, New J. Phys. 13, (2011) 103014.
• [2] R.E. Baumbach, J.J. Hamlin, L. Shu, D.A. Zocco, J.R. O’Brien, P.-C. Ho, and M.B. Maple, Phys. Rev. Lett. 105, 106403 (2010).
• [3] Y. Hirose, K. Arakawa, Y. Kato, Y. Uwatoko, H. Ma, J. Gouchi, F. Honda, and R. Settai, J. Magn. Magn. Mater. 556, 169327 (2022).

Authors

• Y. Hirose^a, K. Arakawa^a, Y. Kato^a, Y. Uwatoko, H. Ma, J. Gouchi, and F. Honda^b, R. Settai^a
• ^aNiigata University
• ^bKyushu University