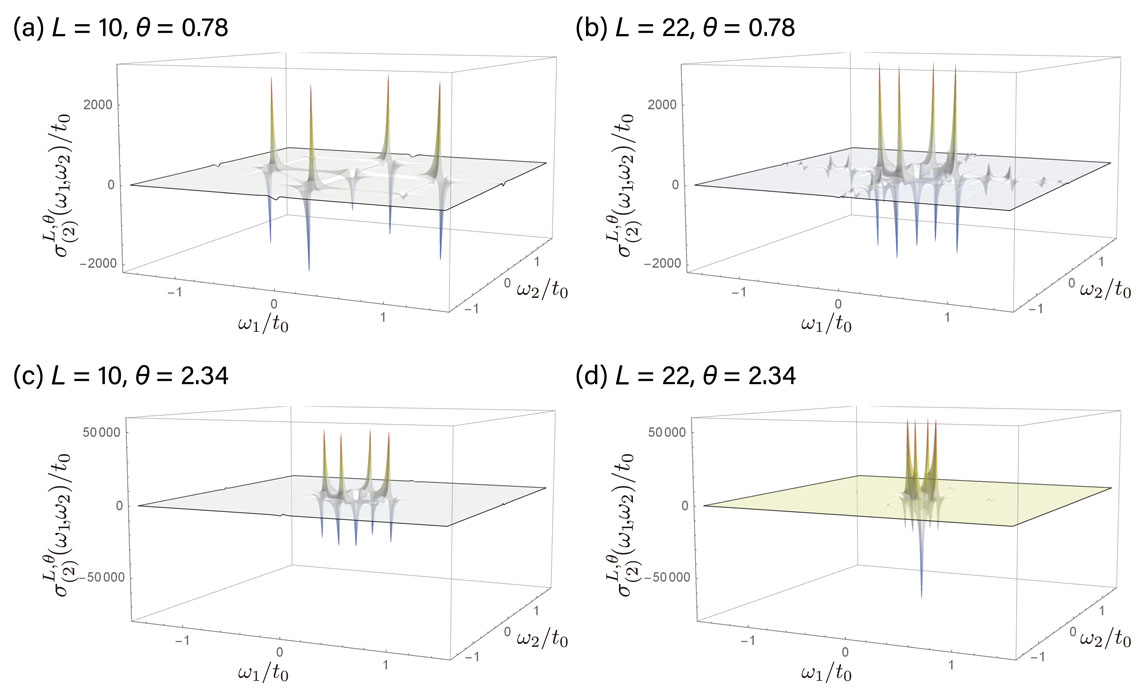
Ballistic transport of a quantum system can be characterized by Drude weight, which quantifies the response of the system to a uniform electric field in the infinitely long timescale. The Drude weight is often discussed in terms of the Kohn formula, which gives the Drude weight by the derivative of the energy eigenvalue of a finite-size system with the periodic boundary condition in terms of the Aharonov-Bohm flux. Recently, the Kohn formula is generalized to nonlinear responses [1,2]. In particular, for the S = 1/2 XXZ chain, analytic expressions of the nonlinear Drude weights are obtained utilizing the Bethe Ansatz exact solution. However, the nonlinear Drude weight determined by the Kohn formula often diverges in the thermodynamic limit. In order to elucidate the issue, in this work [3] we examine a simple example of a one-dimensional tight-binding model in the presence of a single defect at zero temperature. This problem can be formulated in terms of the scattering matrix of the defect. While the bulk energy density and the “defect energy” are non-universal and independent of the Aharonov-Bohm flux, the flux dependence appears in the O(1/L) correction, where L is the system size, which is a universal function of the scattering matrix. This is also consistent with the Conformal Field Theory. Using this formulation, we find that its linear and non-linear Drude weights given by the Kohn formula (i) depend on the Aharonov-Bohm flux and (ii) diverge proportionally to a power of the system size. Since the effect of the Aharonov-Bohm flux on the bulk transport property should vanish in the thermodynamic limit, the dependence on the Aharonov-Bohm flux signals that the non-linear Drude weights thus obtained may not describe the bulk property.

Fig. 1. Second-order optical conductivity of the impurity model for system size L = 10, 22 with the Aharonov-Bohm flux θ, as a function of the two frequencies ω₁ and ω₂. Several peaks are observed near zero frequencies.

We argue that the problem can be attributed to different order of limits. The Drude weight according to the Kohn formula indicates the response of a finite-size system to an adiabatic insertion of the Aharonov-Bohm flux. While it is a well-defined physical quantity for a finite-size system, its thermodynamic limit does not always describe the ballistic transport of the bulk. The pathological behaviors such as the divergence of the nonlinear Drude weights mentioned above are indications of the discrepancy between the bulk transport property and the thermodynamic limit of the Kohn formula.

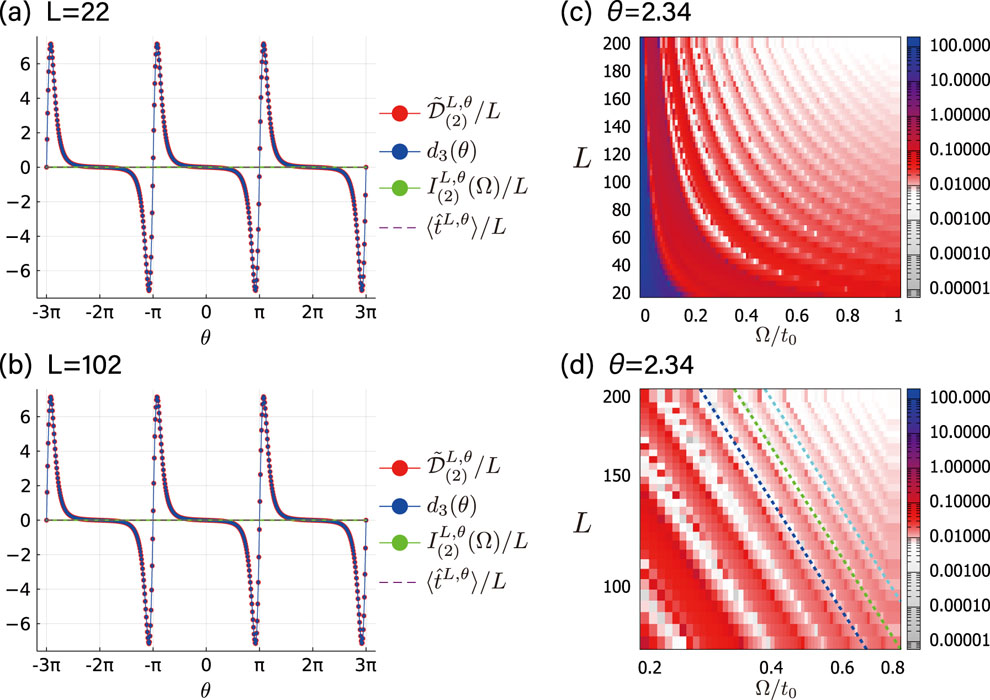
Fig. 2. Comparison between the Kohn formula 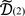and the optical conductivity integrated over a window of low frequencies I₍₂₎, for the second-order Drude weight. While the Kohn formula depends strongly on the Aharonov-Bohm flux θ, the integrated conductivity (almost) vanishes for the entire range of θ. The latter corresponds to the vanishing bulk Drude weight expected in the thermodynamic limit.

In order to clarify the issue, we propose to call the thermodynamic limit of the Kohn formula, namely the Drude weight defined by taking the adiabatic limit before the thermodynamic limit as “Kohn Drude weight”. The ballistic transport of the bulk is rather characterized by the “bulk Drude weight” defined by taking the thermodynamic limit first before the adiabatic (zero-frequency) limit. While the potential issue of the order of limits has been sometimes discussed within the linear response, the discrepancy between the two limits is amplified in nonlinear Drude weights. We demonstrate that, the low-energy excitations of O(1/L) in the finite system of size L, which are excluded from the Kohn–Drude weight, contribute to the bulk Drude weight. This removes the pathological behaviors, making the bulk Drude weight finite and also independent of the Aharonov-Bohm flux.

References

• [1] H. Watanabe and M. Oshikawa, Phys. Rev. B 102, 165137 (2020).
• [2] H. Watanabe, Y. Liu, and M. Oshikawa, J. Stat. Phys. 181, 2050 (2020).
• [3] K. Takasan, M. Oshikawa, and H. Watanabe, Phys. Rev. B 107, 075141 (2023).

Authors

• K. Takasan^a, M. Oshikawa, and H. Watanabe^a
• ^aUniversity of Tokyo