Non-Invertible Duality Transformation Between SPT and SSB Phases
Oshikawa Group
Symmetry-Protected Topological (SPT) phases are one of the central issues in contemporary quantum many-body physics. While the concept of SPT phases was established after the discovery of topological insulators, which are the free electron version of SPT phases, a prototypical example of the bosonic SPT phases, the Haldane gap phase, was found much earlier. In 1992, Kennedy and Tasaki constructed a non-local unitary transformation that maps between a ℤ2×ℤ2 spontaneously symmetry breaking phase and the Haldane gap phase on an open spin chain [1,2]. This gave a unified understanding of the exotic natures of Haldane gap phase, narrowly missing the clear recognition of concept of the SPT phases.
Since the discovery of the concept of the SPT phases in 2009, significant progress has been made on many fronts. In particular, systematic classifications in general dimensions have been studied, uncovering the deep relation to topological quantum field theory and algebraic topology. Given the history, it would be worthwhile to revisit the Kennedy-Tasaki transformation, which played a significant role in understanding the Haldane gap phase 30 years ago, from the modern perspective.
To this end, in this work [3] we demonstrate that the Kennedy-Tasaki transformation can be defined on closed chains by sacrificing unitarity, or by expanding the Hilbert space by including “twist” sectors corresponding to different boundary conditions. This is shown for both the original Kennedy-Tasaki transformation on S = 1 chain and for its generalization on S = 1/2 chain. In both cases, the closed chain version of the Kennedy-Tasaki transformation is a non-unitary transformation and satisfy the non-invertible fusion rules, as in the famous Kramers-Wannier duality transformation. Such non-invertible duality transformations generalizing the Kramers-Wannier duality have been extensively discussed in recent years, both in (1 + 1) and higher dimensions. When the system is invariant under the duality transformation, the operator representing the transformation becomes a non-invertible symmetry of the system. Indeed, we reveal the close connection between the Kramers-Wannier and Kennedy-Tasaki dualities; in particular, we show that Kennedy-Tasaki duality can be constructed in terms of the Kramers-Wannier duality in field theory and on S = 1/2 chain.
Although the Kennedy-Tasaki transformation on S = 1 chain and that on S = 1/2 chain can be shown to be equivalent, the construction on S = 1/2 chain is more convenient for further applications, because the degrees of freedom charged under two ℤ2’s are decoupled; the first and the second groups of S = 1/2 are charged under separate ℤ2’s respectively. Moreover, the decoupling between degrees of freedom admits a more convenient interpretation of twisted gauging, similarly to the Kramers-Wannier duality transformation which implements gauging of the ℤ2 global symmetry. This interpretation also facilitates the construction of new models with interesting topological features. In particular, we utilize Kennedy-Tasaki transformation on S = 1/2 chain to systematically construct a series of gapless SPT phases, not only those have been recently explored, but also uncovering new ones. Our work opens up a new approach to the study of gapless SPT phases, which are at the forefront of the current quantum many-body problem.
References
- [1] T. Kennedy and H. Tasaki, Phys. Rev. B 45, 304 (1992); Commun. Math. Phys. 147, 431 (1992).
- [2] M. Oshikawa, J. Phys. Condens. Matter 4, 7469 (1992).
- [3] L. Li, M. Oshikawa, and Y. Zheng, arXiv:2301.07899 (2023).

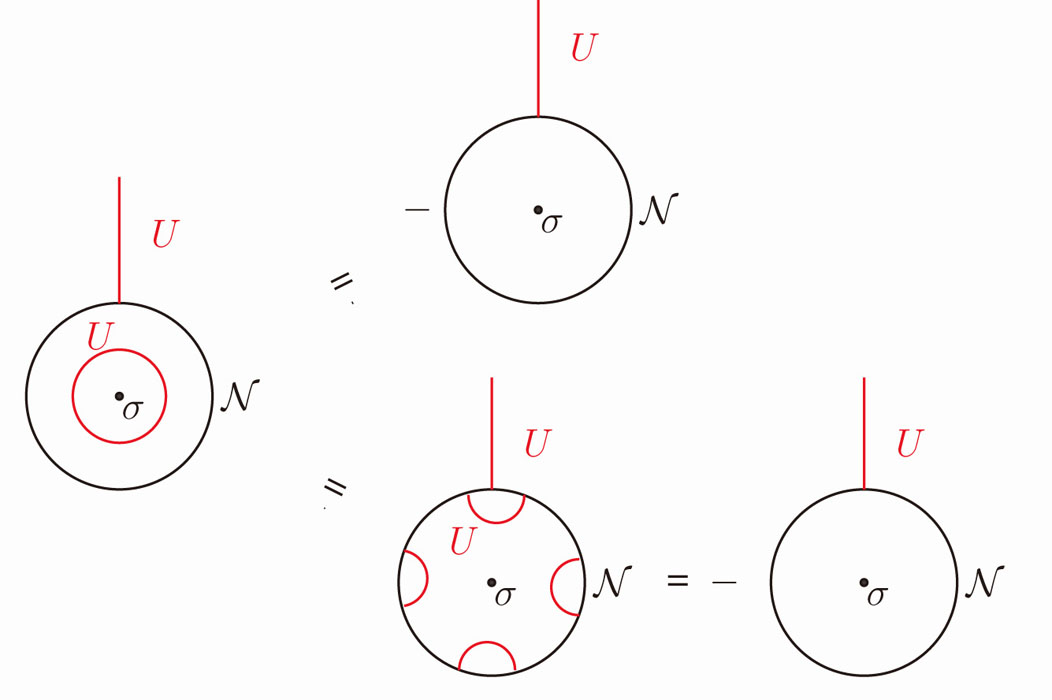
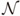 and the global spin-flip operator U in the twisted sector, which is implemented by the twist operator σ. This type of relations is also relevant for Kennedy-Tasaki transformation.
and the global spin-flip operator U in the twisted sector, which is implemented by the twist operator σ. This type of relations is also relevant for Kennedy-Tasaki transformation.