A discrete time crystal (DTC) is an exotic nonequilibrium phase of matter that is realized in periodically driven quantum systems and characterized by the breakdown of the discrete time translation symmetry [1]. The DTC phase has been well studied and experimentally demonstrated in artificial quantum systems without dissipation, such as trapped ions, NV centers in diamonds, and digital quantum computers. However, it had not been explored in solid-state materials, in which unavoidable dissipation is hard to control. Therefore, if one realizes the DTC phase in those materials, it could offer a new possibility of controlling their properties and functionalities.

In this study [2], we have studied the DTC phase in solid-state materials and uncovered its mechanism and properties. We have analyzed a ferromagnetic quantum Ising model periodically driven by a train of magnetic field pulses each corresponding to (nearly) π-pulse (period τ). Using the Floquet-Redfield equation, we have incorporated dissipations due to the couplings of the quantum spins to their surrounding phonon bath. This is much harder to solve than the usual Schrödinger equation because it requires treating a D × D density matrix rather than a D-dimensional wave function (D denotes the Hilbert space dimension, which increases exponentially with the number of spins). To circumvent this problem, we have employed the mean-field theory and numerically obtained the DTC order parameter in a self-consistent manner.

Performing massive numerical calculations on the supercomputer at ISSP, we have determined the DTC phase diagram in solids as shown in Fig. 1. In the normal phase, the system relaxes to a nonequilibrium steady state which oscillates periodically with the same period τ as the drive’s. On the other hand, in the DTC phase, the system turns into a time crystal which oscillates with the doubled period 2τ. These results show that DTCs can be realized in real magnetic materials subject to dissipation at low temperatures if the pulse interval is either long or short enough. Interestingly, this phase diagram highlights a reentrant behavior of the DTC phase as the pulse interval is varied.

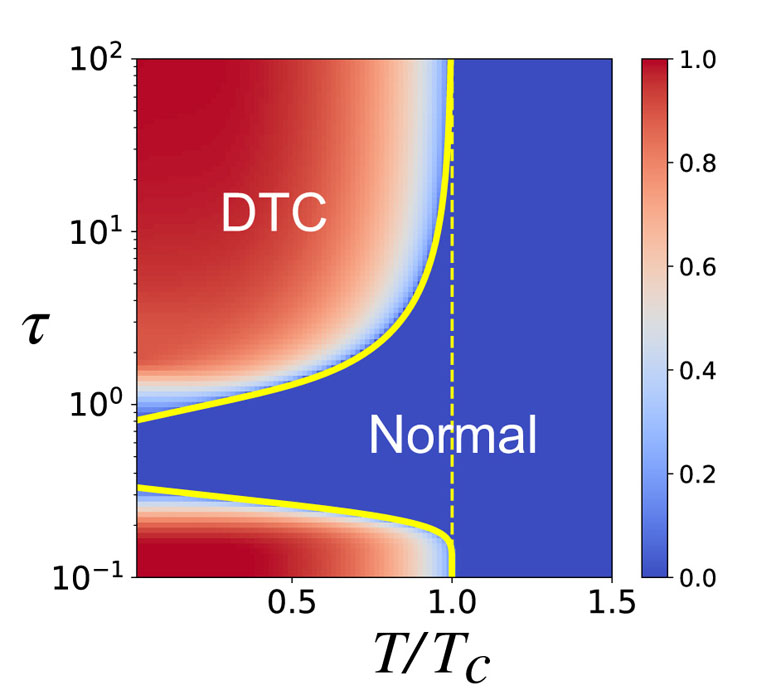
Fig. 1. Phase diagram of the discrete time crystal in solids, and the amplitude of the DTC order parameter is shown by color. The temperature T of the bath is normalized by the equilibrium ferromagnetic transition temperature T_c. τ is the interval between the consecutive pulses in units of J = ħ = 1 (J is the exchange energy).

We have further proposed how to realize and detect the DTC in experiments. We have analyzed the robustness of the DTC against imperfections in pulse shapes unavoidable in experiments such as their height and duration; We have shown that those imperfections do not break the DTC phase. We have also shown that critical phenomena accompany the DTC phase transition. In particular, when temperature is varied to cross the DTC/normal phase boundary, the decay of the DTC order parameter exhibits a power-law in time rather than an exponential. This characteristic behavior can be used as an indicator for the DTC in finite-time experiments. We have finally estimated the parameters for realizing DTC phase and proposed that the electron spin resonance on some magnetic materials may be a promising experimental platform. We believe that these results pave the way for a new research field of time crystals in material science.

References

• [1] K. Sacha and J. Zakrzewski, Rep. Prog. Phys. 81, 016401 (2018).
• [2] K. Chinzei and T. N. Ikeda, Phys. Rev. Research 4, 023025 (2022).

Authors

• K. Chinzei and T. N. Ikeda