Physical properties emerging from the combination effect of electron correlation and spin-orbit coupling have attracted considerable attention in the last decade. In 5d transition metal ions with partially filled t_2g orbital, large spin-orbit coupling of 0.4 eV may entangle the effective orbital angular momentum and the spin angular momentum. The electronic state is described by the effective total angular momentum J_eff. For example, an unpaired electron in the d¹ ion in the cubic octahedral crystal field occupies the J_eff = 3/2 quartet. In solids, interactions among spin-orbital entangled electrons may give rise to exotic ground states such as a spin liquid and multipolar orders. When the d¹ ions with the J_eff = 3/2 state interact on the face-centered-cubic (FCC) lattice, unconventional ground states such as multipolar orders, spin-orbit dimer phase, and spin-orbital liquid may emerge. In the multipolar ordered states, magnetic dipolar, electric quadrupolar, and magnetic octupolar moments can be the order parameter. Magnetic properties of double perovskite-type oxides, chlorides, bromides, and lacunar spinel selenides have been investigated as Mott insulators with the J_eff = 3/2 state on the FCC lattice [1-4]. These examples demonstrate that various multipolar and dimer orders can be realized by applying a certain perturbation via non-magnetic cations and ligand anions.

Another way for exploring a novel electronic phase is applying strong magnetic field comparable to the magnitude of interactions among electrons. In the spin-1/2 Heisenberg model on the tetragonally distorted FCC lattice as seen in the rhenium double perovskite oxides at low-temperature, successive field induced magnetic phases including the 1/2-magnetization plateau may appear in the magnetization process. While the electric quadrupoles do not couple with magnetic field directly, a possibility of magnetic field induced quadrupolar transition has been discussed in CeB₆, where the Ce atom with 4f¹ electron configuration has Γ₈ quartet ground state of which symmetry is identical to the J_eff = 3/2 quartet.

Fig. 1. Magnetization curves of Ba₂CaReO₆ measured up to 66 T (red) and those of relative compounds Ba₂MgReO₆ (blue) and Sr₂MgReO₆ (black).

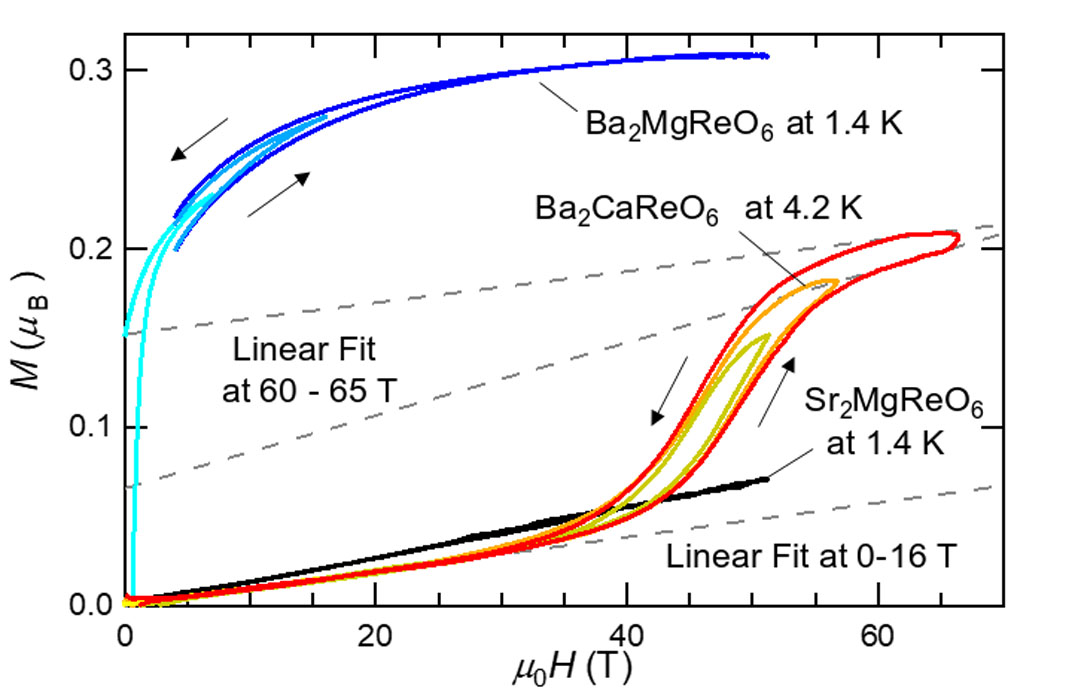
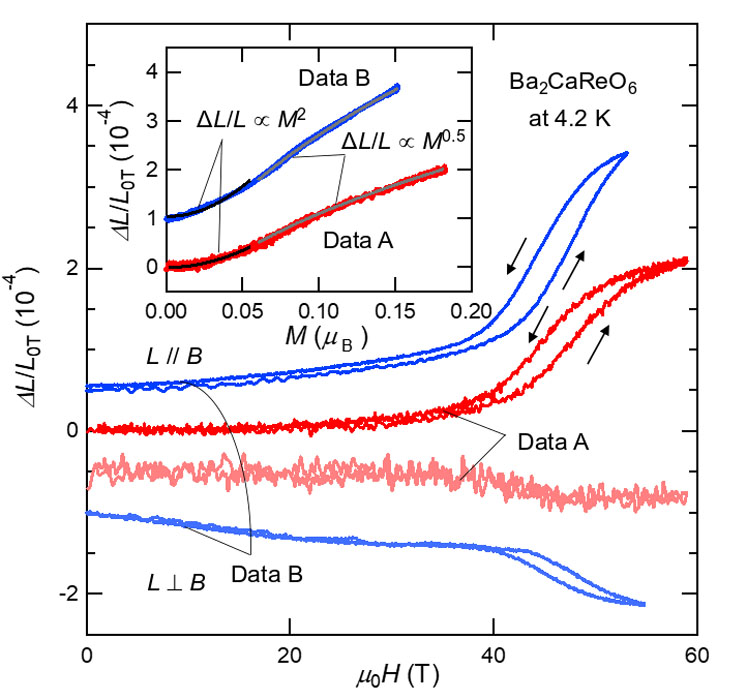
We focused on a rhenium double perovskite oxide Ba₂CaReO₆, which is a candidate of the J_eff = 3/2 Mott insulator with Re⁶⁺ (5d¹) ions. The magnetization of Ba₂CaReO₆ was measured in the pulsed high magnetic field by changing the maximum magnetic field values up to 66 T as shown in Fig. 1 [5]. The magnetization curve at 4.2 K deviates from the linear behavior around 35 T and exhibits a steep increase at around 45 T, indicating the presence of a magnetic field induced phase transition. The full magnetic moment of Ba₂CaReO₆ estimated from the effective magnetic moment is 0.38 μ_B and thus the magnetization of 0.2 μ_B at the high field region is clearly smaller than the full moment. The magnetic field induced phase transition in Ba₂CaReO₆ was also clearly detected in the magnetostriction ΔL/L_0T measured at 4.2 K as shown in Fig. 2. The longitudinal magnetostriction is positive and amounts to 2-3 ×10^-4 at around 60 T, while the transverse magnetostriction is negative and amounts to ~1 ×10^-4 at around 60 T. The longitudinal magnetostriction is plotted against magnetization in the inset of Figure 2. The magnetostriction changes quadratically to magnetization up to around 40 T. The deviation from the quadratic behavior is observed as increasing the field, suggesting a change in the way of spin-lattice coupling via orbital degrees of freedom. The magnetic field induced phase transition is attributed to the transition from the collinear to the canted antiferromagnetic orders with possible changes in the orbital states. Ba₂CaReO₆ would reside in the parameter regime close to the boundary between the two magnetic orders, representing a suitable material for investigating the interplay between the spin-orbital entangled electrons and magnetic field.

Fig. 2. Magnetostriction ΔL/L_0T of Ba₂CaReO₆ measured at 4.2 K. The magnetostriction with positive and negative values correspond to the longitudinal and transverse magnetostriction, respectively. The longitudinal magnetostriction is plotted against the magnetization in the inset.

References

• [1] H. Ishikawa, T. Takayama, R. K. Kremer, J. Nuss, R. Dinnebier, K. Kitagawa, K. Ishii, and H. Takagi, Phys. Rev. B, 100, 045142 (2019).
• [2] H. Ishikawa, T. Yajima, A. Matsuo, Y. Ihara, and K. Kindo, Phys. Rev. Lett. 124, 227202 (2020).
• [3] H. Ishikawa, T. Yajima, A. Matsuo, and K. Kindo, J. Phys.: Condens. Matter 33, 125802 (2021).
• [4] D. Hirai, H. Sagayama, S. Gao, H. Ohsumi, G. Chen, T. Arima, and Z. Hiroi, Phys. Rev. Research 2, 022063 (2020).
• [5] H. Ishikawa, D. Hirai, A. Ikeda, M. Gen, T. Yajima, A. Matsuo, Y. H. Matsuda, Z. Hiroi, and K. Kindo Phys. Rev. B 104, 174422 (2021).

Authors

• H. Ishikawa, D. Hirai, A. Ikeda, M. Gen, T. Yajima, A. Matsuo, Y. H. Matsuda, Z. Hiroi, and K. Kindo