The Berezinskii-Kosterlitz-Thouless (BKT) transition was historically the first example of topological phase transitions, which is now an essential concept in physics as signified by the Nobel Prize in Physics in 2016. The canonical model exhibiting the BKT transition is the classical XY model in two dimensions. The BKT transition is conceptually well understood in terms of the Kosterlitz Renormalization Group (RG) equation. However, the famous “Kosterlitz RG flow” has remained a rather abstract concept, which cannot be seen directly. Moreover, because of the notorious logarithmic corrections, significant finite-size effects persist even in a large system, making conventional finite-size scaling of Monte Carlo methods such as Binder plot powerless. Even with considerable efforts over decades, an accurate determination of the critical temperature remains difficult, even with a huge computational power, for the system as simple as the classical XY model in two dimensions.

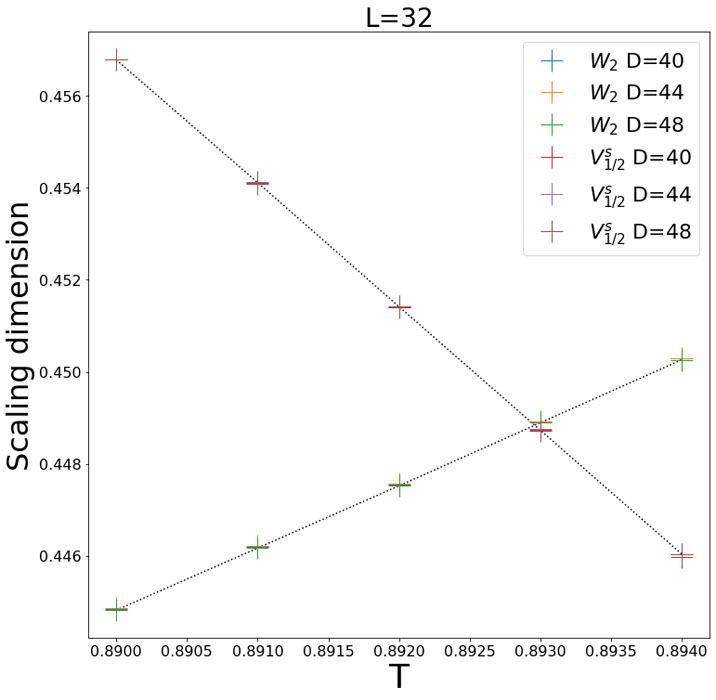
Fig. 1. The “level spectroscopy” applied to the classical two-dimensional XY model with the tensor-network renormalization. The crossing of the two “energy levels” (eigenvalues of the transfer matrix) in a finite-size system gives a precise estimate of the BKT transition temperature, as the logarithmic correction is cancelled out.

On the other hand, many one-dimensional quantum systems can be also described by the same effective theory and thus also exhibit the BKT transition. Interestingly, a powerful numerical finite-size scaling method called “level spectroscopy” was developed specifically for those 1D quantum systems by Okamoto and Nomura. Based on the conformal field theory results on the finite-size energy spectrum thanks to Cardy, they found that the BKT transition can be identified with a level crossing between a certain pair of the energy levels, canceling the logarithmic corrections. This allows a surprisingly accurate determination of the BKT transition point with exact numerical diagonalization of rather small systems. However, the applications of level spectroscopy have been limited to one-dimensional quantum BKT system such as quantum spin chains so far. While it should be applicable to the spectrum of the transfer matrix for the classical two-dimensional XY model, the level spectroscopy has not been applied there, because of the difficulty in calculating the spectrum for the system with continuous variables such as the angle of the XY spin.

Fig. 2. The Renormalization-Group flow for the BKT transition in the classical two-dimensional XY model, constructed numerically from the transfer matrix spectrum based on the combination of tensor-network renormalization and conformal field theory.

In this work, we demonstrated a successful implementation of level spectroscopy on the classical two-dimensional XY model, based on the tensor network renormalization (TNR) scheme. The TNR enables us to obtain a precise spectrum of the transfer matrix, to which the level spectroscopy can be applied. As in the case of the one-dimensional quantum system, it allows a very accurate determination of the critical point by removing the logarithmic corrections from systems of moderate sizes, which can be described by a tensor network with a finite bond dimension. As a result, we have improved the accuracy of the BKT transition temperature in the classical two-dimensional XY model, by an order of magnitude over the best numerical estimate in the literature.

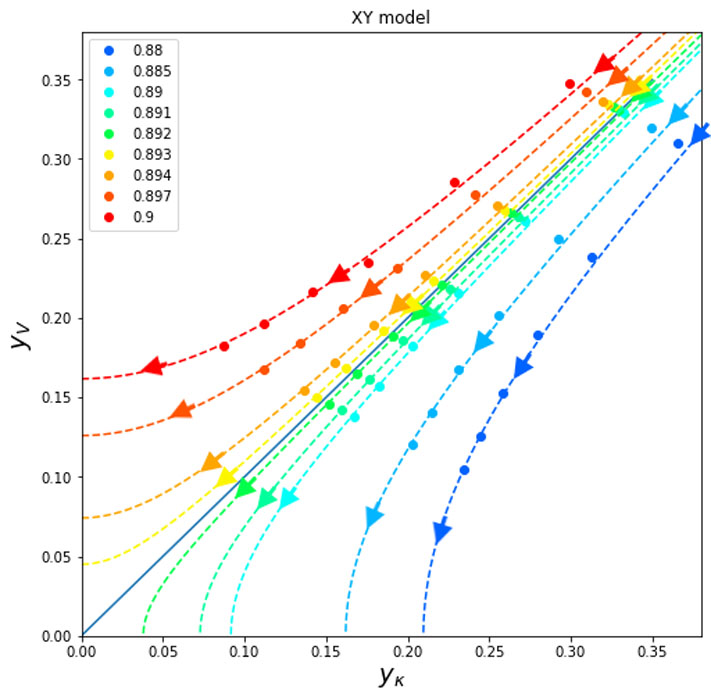
Furthermore, our TNR study covers larger system sizes than those in the existing level spectroscopy studies on one-dimensional quantum systems. We found a new feature of the finite-size scaling, that leads to a further improvement of level spectroscopy. Finally, we also applied our methodology to visualize the celebrated Kosterlitz RG flow of the BKT transition based on the numerical data, for the first time to our knowledge.

References

• [1] A. Ueda and M. Oshikawa, Phys. Rev. B 104, 165132 (2021). [Editor’s Suggestion]

Authors

• A. Ueda and M. Oshikawa