Domain Walls (DW) are topological defects with mesoscopic size and understanding their dynamics is important for both experimental and theoretical interests. We have theoretically studied the steady state dynamics of DW driven by magnetic field in a system with multiple orders coexist [1].

Fig. 1. Velocity of composite DWs driven by magnetic field expanded in H. α is the linear mobility. c is the interaction strength.

Our target system is the multiferroic compound FeGdO₃ and its low-temperature phase is characterized by three order parameters: antiferromagnetic moments of Fe spins N with biaxial anisotropy and isotropic Gd spins n and one component of electric polarization P. Their coupling cN∙nP leads to composite DWs, i.e. two order parameters need to flip together in each DW, and therefore there exist 3 different types of composite DWs: N-n, N-P, and n-P.

Fig. 2. Stability phase diagram of composite DWs driven by magnetic field H. B: N-n DW is unstable, C: N-P DW is unstable, A: both DWs are stable.

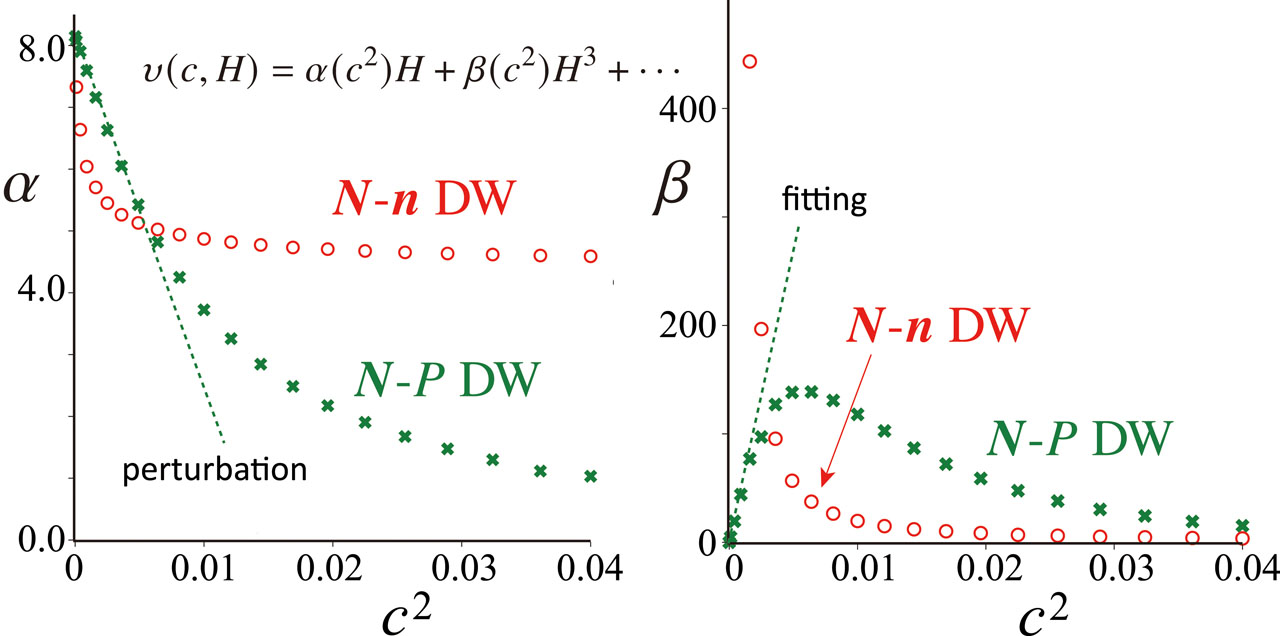
We have studied the dynamics of these composite DWs driven by magnetic field based on the phenomenological time-dependent Ginzburg-Landau theory. Neglecting fluctuations inside the DW, we have investigated by numerical calculations the time evolution of their one-dimensional motion. With the help of anisotropic exchange couplings, the applied magnetic field couples to N and thus drives N-P and N-n DWs. One important finding is the difference between these two types in the scaling of DW steady state velocity υ(c,H). In its weak field expansion υ(c,H) = α(c²)H+β(c²)H³+…, the coefficients exhibit a singularity at c = 0 for N-n DW, and this is related to n’s internal isotropy.

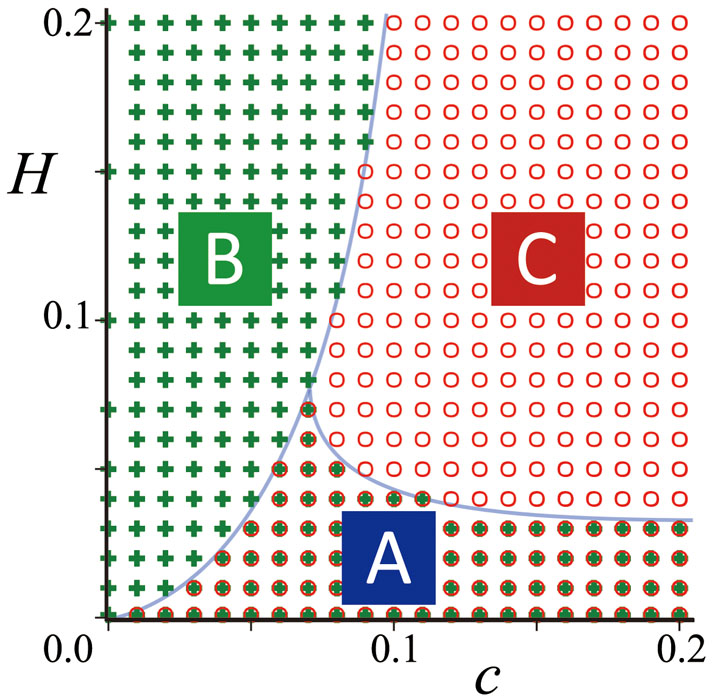
As a big surprise, it turns out that a composite DW becomes unstable in strong magnetic field and splits into a pair of different types: N-P → N-n + n-P and N-n → N-P + n-P. In both cases, n-P DW is immobile but its partner succeeds to the moving part after splitting. The possibility of this type of splitting was pointed out as an impurity effect [2], but we have found that it may occur in a pure bulk as a dynamical instability. An important point is that the non-flipping component is also dragged by the flipping ones due to the coupling c-term. With increasing the driving field, its modulation grows and finally creates a pair of kink and anti-kink, which is DW splitting. This type of dynamical instability may appear, in principle, in any systems with more than two types of order parameters. It is an interesting challenge to observe in experiments this splitting of composite DW.

References

• [1] K. Kawahara and H. Tsunetsugu, J. Phys. Soc. Jpn. 90, 014703 (2021).
• [2] Y. Tokunaga et al., Nat. Mater. 8, 558 (2009).

Authors

• H. Tsunetsugu, K. Kawahara