Non-trivial topology in a condensed-matter state realizes a quantization of a physical quantity. One of the most fundamental examples is the quantized Hall conductivity in a quantum Hall system, where the quantized Hall conductivity is given by the Chern number determined by the topology of the system.

A new intriguing case of this topological quantization is now found in a magnetic insulator, a Kitaev magnet. In the Kitaev model, localized spin-1/2 moments on a two-dimensional (2D) honeycomb structure are coupled each other by bond-dependent Ising interactions. The frustration effect of this Kitaev Hamiltonian prevents the spins from ordering even at the zero temperature, realizing a quantum spin liquid state. Remarkably, this ground state of the Kitaev Hamiltonian is exactly solvable. The ground state has been shown to be characterized by the two kinds of elementary excitations; itinerant Majorana fermions and localized Z₂ fluxes. In a magnetic field, this itinerant Majorana fermions have topologically non-trivial gapped bands with the Chern number C = ±1, giving rise to a quantized chiral edge current protected by the field-induced gap. In contrast to a quantized chiral edge current of electrons in a quantum Hall system, this chiral edge current is carried by the charge neutral Majorana fermions. Therefore, this quantized chiral edge current has been predicted to appear in the 2D thermal Hall conductivity as κ^2D_xy/T = q_tC/2, where q_t = (π/6)k²_B/ħ.

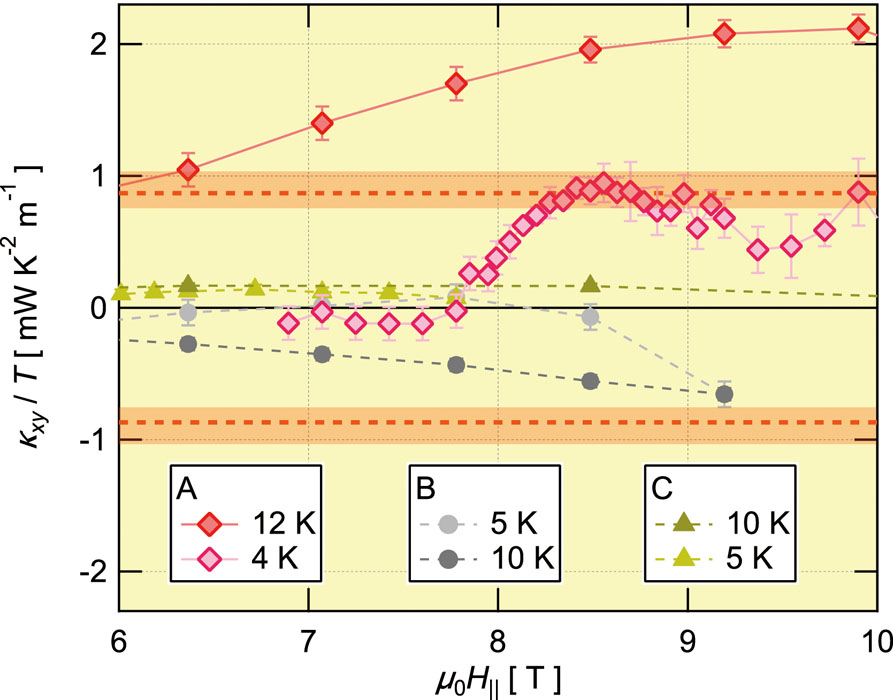
In this work [1], we reveal that it is necessary to protect the chiral edge current from severe scattering effects on phonons to stabilize the quantized thermal current. We investigate the sample dependence of the longitudinal (κ_xx) and transverse (κ_xy) thermal conductivity of three single crystals of α-RuCl₃ – a promising candidate realizing the Kitaev spin liquid [2]. We find the half-integer quantized thermal Hall effect in a sample showing the largest κ_xx among the three crystals (sample A in Fig. 1). On the other hand, the other samples with smaller κ_xx show κ_xy much smaller than the value expected for the quantization (Fig. 2). Given that κ_xx is mostly given by phonons, the different magnitudes of κ_xx in different samples reflect the different scattering strengths on phonons; phonons in a sample with smaller κ_xx are exposed in stronger scattering effects. Therefore, the dependence of κ_xy on κ_xx shows that the chiral edge current in the Kitaev magnet is sensitive to scattering effects on phonons.

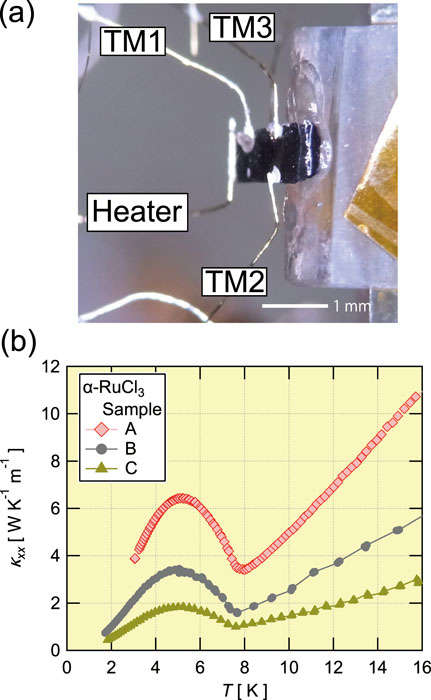
Fig. 1. (a) A setup picture of the thermal conductivity (κ_xx) and the thermal Hall (κ_xy) of α-RuCl₃ (sample A). The sample was tilted to the base plate so that the magnetic field oriented to 45 degree to the c axis. (b) The temperature dependence of κ_xx of different samples (A, B, and C) at zero field.

Fig. 2. The in-plane field dependence of κ_xy⁄T of all the samples. The dotted lines show the value corresponding to the half-integer quantized thermal Hall effect κ^2D_xy/T = q_tC/2, where q_t = (π/6)k²_B/ħ. The sign of κxy of sample A is inverted for a clarity.

Further, we find that a sample with a larger κ_xx shows a larger decrease of the magnetic susceptibility below the Néel temperature, in addition to a larger field-increase effect of κ_xx, showing that magnetic scattering effects are more strongly suppressed by magnetic fields in a sample with a better quality. These results suggest that suppressing this magnetic scattering effect plays an important role to realize the quantized thermal Hall effect.

References

• [1] M. Yamashita et al., Phys. Rev. B 102, 220404(R) (2020).
• [2] Y. Kasahara et al., Nature 559, 227 (2018).

Authors

• M. Yamashita, J. Gouchi, Y. Uwatoko, N. Kuritaa, and H. Tanaka^a
• ^aTokyo Institute of Technology