More than six decades have passed since Anderson’s seminal paper on localization. During the subsequent decades, there have been numerous important discoveries including weak localization, universal conductance fluctuations, and the scaling theory of localization. Since the proposal of the scaling theory, determining the critical behavior of the localization-delocalization transition, which is usually referred to as the Anderson transition (AT), has continued to attract considerable attention.

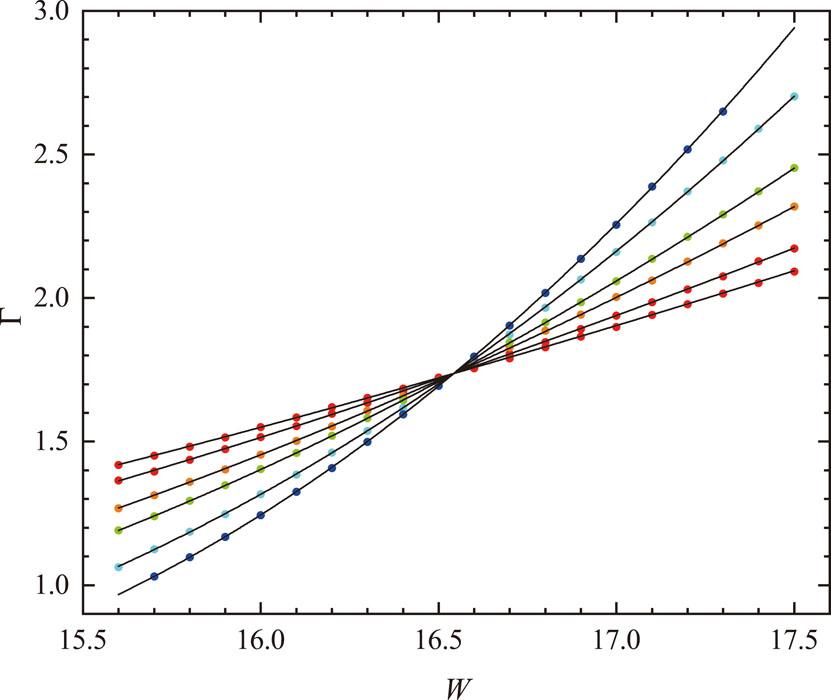
One of the most widely used approaches to study the AT quantitatively is to calculate the Lyapunov exponents (LE’s) and to analyze them using finite size scaling. Large scale computations using the supercomputer System B at ISSP have enabled us to calculate LE’s with high precisions for very large system sizes. We consider a system of size L_x × L × L, which we divide into layers of an L × L square. The transfer matrix M relates the wave functions on the 1^st layer to L_xth layer, and the LE’s are the eigenvalues of the matrix 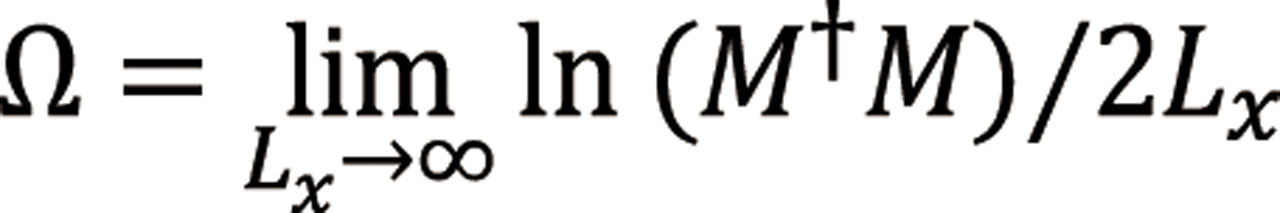. From the smallest positive LE, γ, we define a quantity Γ = γL.

The conventional method requires the simulation of a single very long sample. While this method has been employed very successfully in numerous simulations over the preceding decades [1], the calculations are inherently serial and do not allow us to take advantage of massively parallel computing. We devised an alternative method to simulate an ensemble of much shorter samples and take an ensemble average, allowing us to make full use of System B.

We have analyzed the LE’s using finite size scaling, and estimated the critical exponent for the divergence of the correlation length, ν = 1.572 [1.566,1.577] for three dimensional (3D) Anderson model of localization [1,2], H = Σ_iε_i | i 〉〈 i | −Σ_〈i,j〉 | i 〉〈 j |, where ε_i is the onsite random potential distributed uniformly in [-W⁄2, W⁄2]. We fit the W and L dependence of Γ using finite size scaling (Fig. 1).

Fig. 1. Γ as a function of the disorder strength W in the 3D Anderson model of localization for various cross section size L = 12.18, 24, 32, 48 and 64. L = 96 is underway using new System B.

The critical exponent changes when a magnetic field is applied. This can be realized by inserting Peierls phase in the nearest neighbor transfer. We obtain ν = 1.443 [1.437,1.449] which is distinctly different from the case without a magnetic field [3].

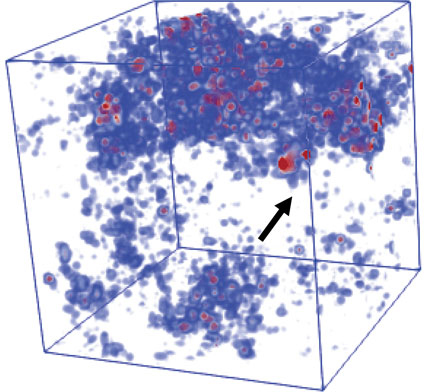
At the critical point, the wave functions exhibit multifractality, hence the local density of states fluctuates significantly. If we consider dilute magnetic impurities, the Kondo temperature T_K varies from one magnetic impurity to another due to the large fluctuations of wave functions (Fig. 2). We have calculated the local density of states at the critical point using the kernel polynomial method and calculated the Kondo temperature distribution [4]. The massively parallel calculations on System B enabled us to reach the small T_K needed to check the analytic prediction.

Fig. 2. Schematic of a magnetic impurity and a multifractal wave function.

In addition to the cases of Anderson’s model of localization with and without magnetic fields, depending on whether we have spin-rotation symmetry, chiral symmetry as well as particle-hole symmetry, we have 10 symmetry classes for random quantum systems. In recent years, the non-Hermitian systems with randomness, which are classified into 38 symmetry classes, are attracting renewed interests. We have studied the critical behaviors of AT with chiral and/or particle-hole symmetries [5], and most of the critical exponents for the AT in 3D are now determined. In addition, we have verified that the transfer matrix method and the finite size scaling work for non-Hermitian systems. We are now studying the localization-delocalization transition for non-Hermitian systems [6,7] and determining the critical exponents, which might explain the critical behavior of light localization.

References

• [1] K. Slevin and T. Ohtsuki, New J. Phys. 16, 015012 (2014).
• [2] K. Slevin and T. Ohtsuki, J. Phys. Soc. Jpn. 87, 094703 (2018).
• [3] K. Slevin and T. Ohtsuki, J. Phys. Soc. Jpn. 85, 104712 (2016).
• [4] K. Slevin, S. Kettemann, and T. Ohtsuki, Eur. Phys. J. B 92, 281 (2019).
• [5] X. Luo, B. Xu, T. Ohtsuki, and R. Shindou, Phys. Rev. B 101, 020202 (2020).
• [6] X. Luo, T. Ohtsuki, and R. Shindou, Phys. Rev. Lett. 126, 090402 (2021).
• [7] X. Luo, Z. Xiao, K. Kawabata, T. Ohtsuki, and R. Shindou, arXiv:2105.02514.

Authors

• T. Ohtsuki^a and K. Slevin^b
• ^aSophia University
• ^bOsaka University