Magnetoresistance is one of the fundamental phenomena in the research field of spintronics. Recently, a novel type of magnetoresistance called spin Hall magnetoresistance (SMR) has been observed in a bilayer system composed of a normal metal (NM) and a ferromagnetic insulator (FI) [1]. SMR is explained by the combination of charge-spin conversions in NM and loss of spins at the NM/FI interface [1,2] (see Fig. 1 (a)). When an in-plane charge current is applied to the NM layer with a large spin-orbit interaction, spin accumulation is caused near the NM/FI interface by the spin Hall effect. The amount of spin accumulation is affected by the orientation of FI magnetization because it changes the rate of spin loss at the interface. A backward spin current owing to spin diffusion is converted into the charge current again by the inverse spin Hall effect and induces longitudinal magnetoresistance, which depends on the orientation of FI magnetization. Recently, SMR has been reported for the bilayer system composed of NM and an antiferromagnetic insulator (AFI) [3], where the orientation of the Néel vector of AFI has been changed by the orientation of magnetization of FI using the NM/AFI/FI trilayer structure.

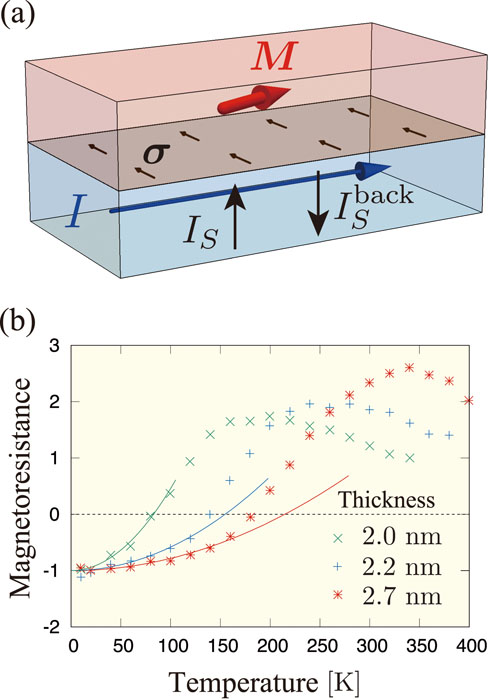
Fig. 1. (a) Schematic diagram of the normal-metal(NM)/ferromagnetic-insulator(FI) bilayer system for the spin Hall magnetoresistance (SMR) measurement. (b) Experimental data of SMR measured in Pt/NiO/YIG bilayer systems. The data is normalized as −1 at zero temperature using the extrapolated value by the fitting.

SMR can be described theoretically by combining the spin diffusion theory with the boundary condition at the interface in terms of the spin-mixing conductance [2]. However, in this theory, the spin-mixing conductance at the interface is a phenomenological parameter that has to be determined experimentally; therefore, its temperature dependence cannot be predicted. Furthermore, the magnetization-orientation dependence of the spin-mixing conductance is assumed phenomenologically by its definition. This semiclassical description of SMR seems to be insufficient for studying quantum features of magnetic insulators such as the effect of thermally excited magnons.

In our work, we constructed a microscopic theory of SMR and derived a general formula of a spin conductance at the interface for both NM/FI and NM/AFI bilayer systems in terms of spin susceptibilities. We clarified that the spin current is composed of static and dynamic parts. The static part of spin current originates from spin flip owing to an effective magnetic field induced by an interfacial exchange coupling. This part is almost independent of the temperature, and takes a maximum when the magnetization (or the Néel vector) is perpendicular to accumulated spins in a normal metal, which is consistent with intuitive discussions in previous experimental studies. However, the dynamic part, which is induced by creation or annihilation of magnons, depends on the temperature, and has opposite magnetization dependence, i.e., takes a maximum when the magnetization (or the Néel vector) is parallel to accumulated spins in a normal metal. The dynamic part becomes larger when the amplitude of the localized spin, S₀, is smaller. This indicates that the sign of SMR changes at a specific temperature if S₀ is sufficiently small. In Fig. 1 (b), we show the measured temperature dependence of SMR in Pt/NiO/YIG bilayer systems [3]. The sign of SMR changes at 80, 140, and 180 K for NiO thickness of 2.0, 2.2, and 2.7 nm. In addition, we show the fitted curve in the figure using quadratic temperature dependence that is predicted by our theory. This fitting indicates that the quadratic temperature dependence explains well the experimental data at low temperatures. We also derived the Onsager relation between spin conductance and thermal spin-current noise.

This study has been performed as a joint study with Mamoru Matsuo, who was a visiting professor of ISSP in the academic year 2016.

References

• [1] H. Nakayama et al., Phys. Rev. Lett. 110, 206601 (2013).
• [2] Y. T. Chen et al., Phys. Rev. B 87, 144411 (2013).
• [3] D. Hou et al., Phys. Rev. Lett. 118, 147202 (2017).
• [4] T. Kato, Y. Ohnuma, and M. Matsuo, Phys. Rev. B 102, 094437 (2020).

Authors

• T. Kato, Y. Ohnuma^a, and M. Matsuo^a
• ^aKavli Institute for Theoretical Sciences