Quadrupole Orders in Pr-Based Compounds with fcc Lattice Structure
H. Tsunetsugu, T. Ishitobi, and K. Hattori
Recently, physical properties of electric quadrupoles in PrMgNi4 were studied experimentally and their antiferro ordering has been discussed [1]. Praseodym ions constitute a frustrated structure of fcc lattice, and little had been known for its ordered quadrupolar pattern. Studying this issue theoretically, we have identified various ordered patterns and determined the phase diagram [2].
Fig. 1. Phase diagram of the J-K-Δ model for electric quadrupoles on the fcc lattice at temperature T = 0.1Δ. See Ref.2 for details of ordered phases.
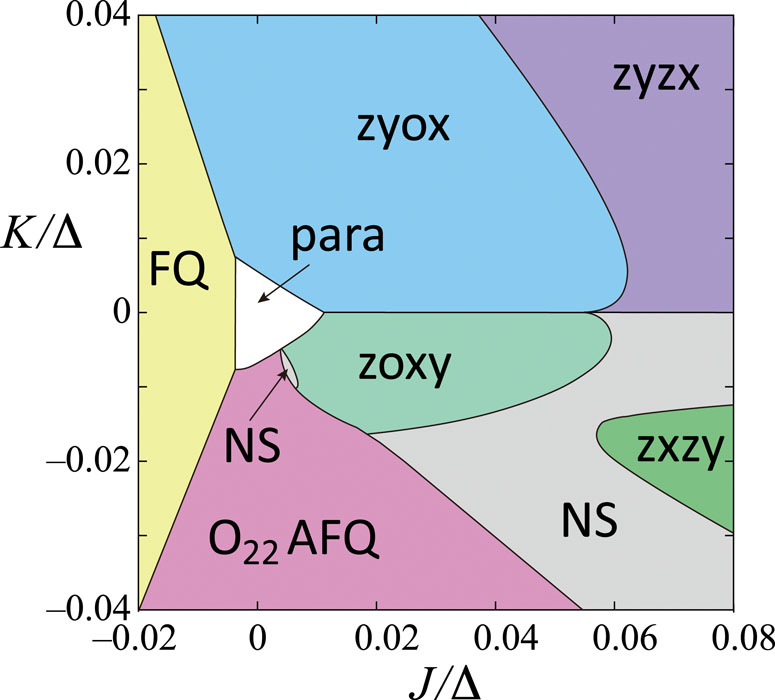
A non-Kramers doublet is the ground state of Pr3+ ion in a crystal field with cubic symmetry, and two components of electric quadrupole are active therein: O20 and O22 with symmetry z2 and x2–y2, respectively. Despite the same number of degrees of freedom, ordering of those quadrupoles may show different features from those in easy-plane magnets due to two reasons. First, while magnetic moments are axial vectors, electric quadrupoles are second-rank tensors, and therefore their effective interactions have a different form. We have determined its minimal form with two parameters J and K corresponding to isotropic and anisotropic couplings. The second reason is the presence of a third order Z3 anisotropy which time-reversal symmetry prohibits for magnetic moments. This is induced by a hybridization of a singlet excited state, and its excitation energy Δ is another control parameter of this system.
Fig. 2. Structure of electric quadrupoles in the zyox phase. Quadrupoles are not ordered on the corner sites.
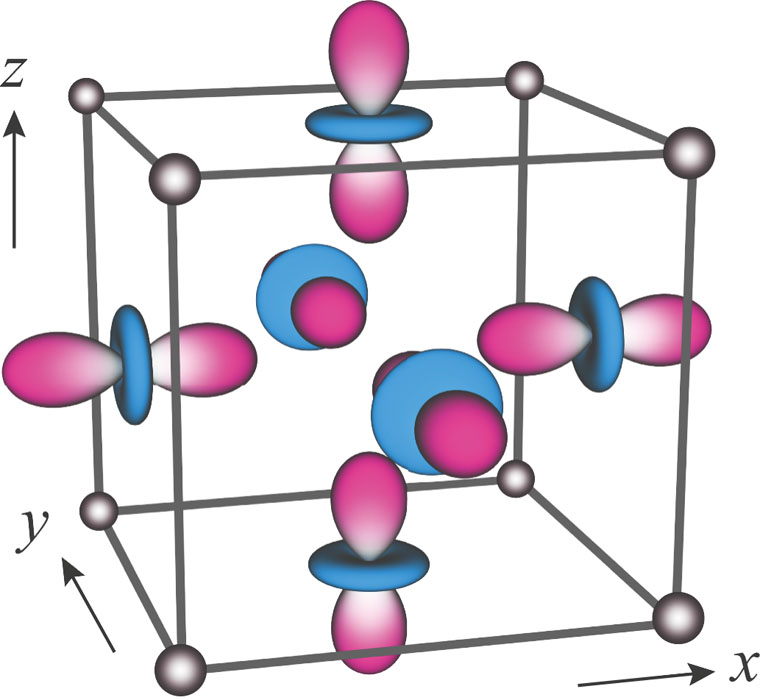
We have employed a mean field approach with a four-site unit and determined the phase diagram at zero and finite temperatures. In the limit of Δ → ∞, the Z3 anisotropy vanishes and three ordered phases appear at low temperatures depending on the ratio of J and K: O20 ferro, O20 antiferro, and O22 antiferro. For Δ < ∞, the Z3 anisotropy takes effects and this leads to a phase diagram with rich structure. Related to induced canting of O22 components, the most important result is the instability of the two-site antiferro orders to more complex four-site structures. It is also interesting that two of the new phases (zyox and zoxy) exhibit a partial order in which one sublattice remains disordered and quadrupole is polarized as x2, y2, and z2 in each of the other three sublattices. They are a triple-q order in which three components with different polarizations and wave vectors are coupled by the Z3 anisotropy, and we have confirmed their stability by a phenomenological Landau theory. Thus, we have established the basic picture of the phase structure for quadruple orders, and hope that this encourages further experimental studies as well as more advanced theoretical analysis on this issue.
References
- [1] Y. Kusanose et al., J. Phys. Soc. Jpn. 88, 083703 (2019); Y. Kusanose et al., JPS Conf. Proc. 30, 011160 (2020).
- [2] H. Tsunetsugu, T. Ishitobi, and K. Hattori, J. Phys. Soc. Jpn. 90, 043701 (2021).