Kadanoff’s block-spin method gives a simple physical picture for the general RG transformations. Combined with Migdal’s bond-moving trick, it serves as the first approximation that allows us direct estimation of the critical exponents, though the accuracy may not be satisfactory in many cases. However, it is not obvious how we can systematically improve on it so that eventually we can obtain, at least in principle, estimates as accurate as we like. Modern tensor-network (TN)-based methods, such as tensor renormalization group (TRG), tensor network renormalization (TNR), loop-TNR, high-order TRG (HOTRG), etc, opened up new possibilities for the RG transformations. Generalizing the conventional real-space RG (RSRG) transformations, they are more versatile and, more importantly, systematically improvable. The free energy, the energy, the magnetization, or any other locally defined order parameters can be computed by one of those methods. As for the estimation of the scaling dimensions, the CFT-based transfer-matrix method based on the conformal-field theory has been widely used for two-dimensional classical systems. For higher dimensions, however, the only method generally applicable was to esimate the correlation functions and apply the finite-size scaling to them. This indirect method may be good for obtaining one or two scaling dimensions, but it is obviously not a systematic way for obtaining a series of scaling dimensions.

Conceptually, it is straight-forward to construct a method for obtaining the series of scaling dimensions from any RSRG method. Simply we can expand the renormalized tensor with respect to the preceding tensor, i.e., the tensor at one RG step before the current one (Fig. 1). At the fixed point, the linear term would produce the scaling dimensions as its eigenvalues. This is exactly what we learn from textbooks for obtaining the scaling dimensions, in many cases with the Migdal-Kadanoff (MK) approximation as an example. In the MK approximation for the Ising model, we have only two independent fields, and it is impossible to obtain more than two scaling dimensions, whereas in the general TN-based method, we have as many fields as we like and, accordingly, we can in principle obtain many scaling dimensions systematically from the same calculation. However, it has been hard to carry out this straight-forward textbook program in practice because of the influence of the short-range entanglement.

Fig. 1. Schematic diagram of the linearized tensor RG equation "R". In the proposed method, it can be generated using automatic differentiation once the coarse graining is implemented.

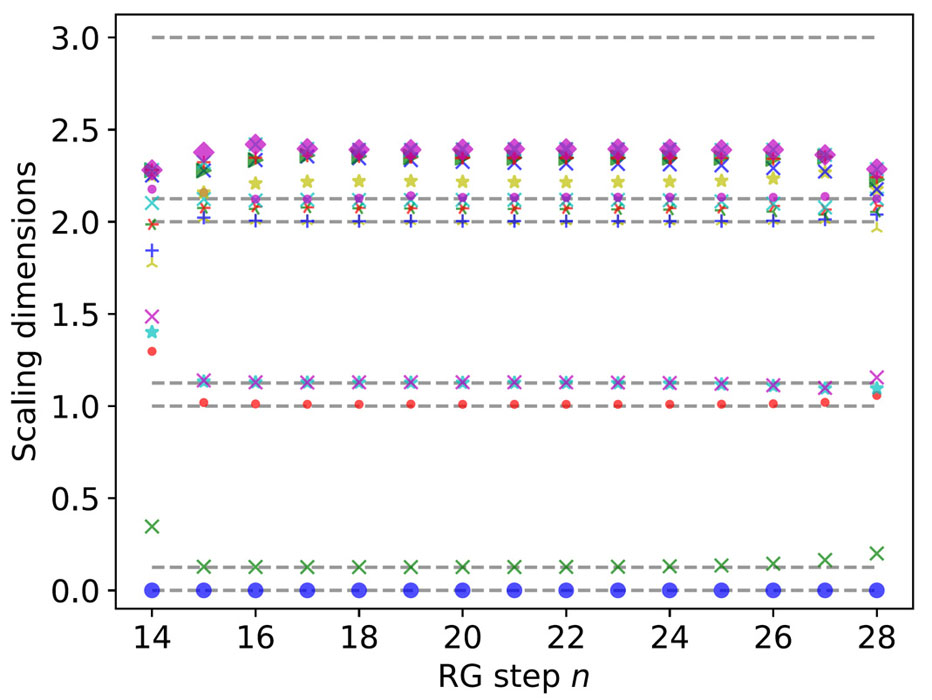
In the paper [1], we adopted the graph-independent local truncation (GILT) method to eliminate the short-range entanglement. This made it possible to fully exploit the RG interpretation of various tensor-network-based methods and show a way to carry out the above-mentioned textbook RG prescription in the TN language: identify a fixed point, linearize the RG equation around this fixed point, and diagonalize it to obtain scaling dimensions. For the RSRG, we used HOTRG though it is not the only possible choice. As shown in Fig. 2, our benchmark calculation on the 2D classical Ising model shows that the proposed method works equally well compared with the above-mentioned CFT-based transfer matrix. The advantage of the present scheme is its potential applications to 3D systems, where the CFT-based method is inapplicable.

Fig. 2. The scaling dimensions of the 2D Ising model obtained directly from the linearized RG plotted against the number of RG steps applied at the critical point. The flat region represents the fixed point values.

References

• [1] X. Lyu, R. G. Xu, and N. Kawashima, Phys. Rev. Research 3, 023048 (2021).

Authors

• X. Lyu, R. G. Xu^a, and N. Kawashima
• ^aThe University of Tokyo