The hexagonal antiferromagnet Mn3Sn with triangular spin structure exhibits large spontaneous electronic responses associated with Weyl fermions [1], which has attracted tremendous attention due to its potential for spintronic applications [2]. The single crystals of this compound are known to be stable in their off-stoichiometric compositions. Depending on the composition, three distinct kinds of magnetic phases can emerge as a function of temperature, namely the high-temperature triangular spin structure phase (q = 0) [3], the intermediate-temperature incommensurate spin spiral phase (q ≠ 0) [4], and the low-temperature cluster spin glass phase [5]. The topological transport properties vanish in the incommensurate phase, whose origin remains elusive. A theoretical study suggests that out-of-plane antiferromagnetic exchange interaction may destabilize the triangular spin structure [6].

A long-wavelength incommensurate spin structure can originate from various mechanisms, such as competition between short-range and long-range exchanges in CeSb [7], and Fermi surface nesting in hexagonal rare-earth elemental metals [8]. In the latter case, Fermi surface nesting is largely determined by the lattice constant ratio c/a, which is tunable by alloying or uniaxial pressure. Uniaxial pressure is a clean tuning parameter compared to chemical doping. Here, we explore the evolution of the magnetic phase diagram of Mn₃Sn under c-axis uniaxial pressure.

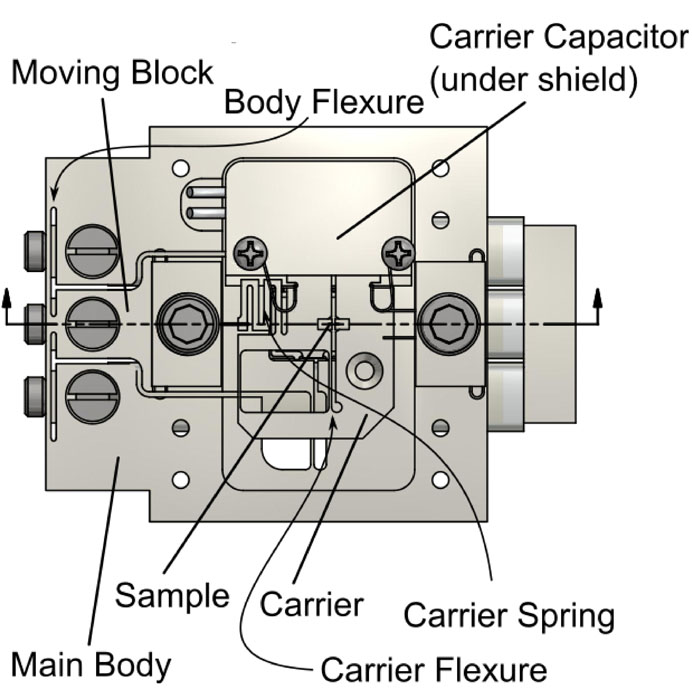
In collaboration with Dr. Clifford Hicks and Dr. Kent Shirer from Max Planck Institute for Chemical Physics of Solids (MPI CPfS), Dresden, Germany, we developed a piezoelectric-based uniaxial stress dilatometer that provides in-situ stress tunability, as shown in Fig 1. This device allows high-sensitivity thermal expansion measurements, offering a compelling route to thermodynamic information on magnetic phase evolution under large and homogenous applied stress. The sample is sculpted into a paddle using a focused ion beam and then epoxied across the central gap of the sample carrier, as seen in the inset of Fig 1a. Applying voltage to the piezo stacks displaces a spring and delivers uniaxial stress to the sample, while the sample’s length change was estimated from the displacement of the parallel plate capacitor attached to the carrier.

Fig. 1. Uniaxial stress dilatometer

Figure 2a shows the temperature dependence of c-axis length change L-L₀ of Mn₃Sn at various applied uniaxial forces. At zero force, the sample exhibits a first-order transition from triangular to spiral spin structure on cooling below T_H = 267 K, accompanied by a discontinuity in L-L₀. Under uniaxial force, the transition splits into two, as shown in Fig. 2b. The peak in –dΔL/dT that shifts to lower temperatures with an increasing uniaxial force corresponds to the response of the central narrow portion of the sample. With an elastic compressive stress of σ_z ~-1.5 GPa, the transition is suppressed by ∆T ~ -50 K. Below -σ_z ~ 0.5 GPa, T_H has a linear dependence on σ_z, with ∂T_H/∂σ_z = 33.3 K at zero stress. We estimate an entropy change of ΔS ~ 0.1 mJ mol^-1 K^-1 from Clausius-Clapeyron relation, using the magnitude of the discontinuity in ΔL and ∂T_H/∂σ_z. This value of ΔS is consistent with that estimated from heat capacity data. Above -σ_z ~ 0.5 GPa, ∂T_H/∂σ_z does not deviate appreciably from its ambient pressure value; this information cannot be extrapolated solely based on the zero pressure ∂T_H/∂σ_z. Overall, we found that the transition is insensitive to stress compared with its response to chemical doping, suggesting that the lattice is not the primary driver of the transition. This device is compatible with other probes, such as transport and spectroscopy, opening a new avenue to study phases of matter under extreme conditions [9].

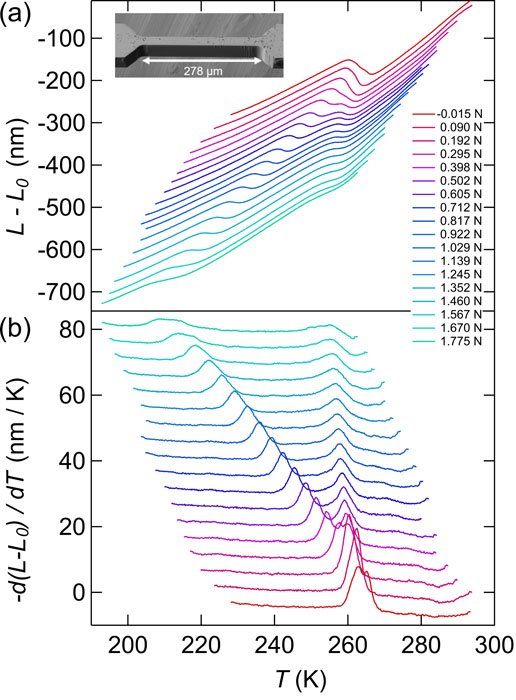
Fig. 2. Thermal expansion of Mn₃Sn under uniaxial pressure. (a) Sample’s c-axis length change L-L₀ vs. temperature under various applied uniaxial forces. Inset shows the sample used for the measurements. (b) Derivative of c-axis length change -d(L-L₀)/dT vs. temperature (bottom panel) under various applied uniaxial forces.

References

• [1] T. Chen, T. Tomita, S. Minami, M. Fu et al., Nat. Comm. 12, 572 (2021).
• [2] H. Tsai, T. Higo et. al., Nature 580 (2020).
• [3] T. Nagamiya, S. Tomiyoshi, and Y. Yamaguchi, Solid State Commun. 42 (1982).
• [4] J.W. Cable et. al., Solid State Commun. 88 (1983).
• [5] W. J Feng, D. Li et. al., Phys. Rev. B 73 (2006).
• [6] S. Dasgupta and O. Tchernyshyov, Phy. Rev. B 102 (2020).
• [7] M. E. Fischer and W. Selke, Phys. Rev. Lett. 44 (1980).
• [8] A. Andrianov et. al., Phys. Rev. B 62 (2000).
• [9] M. Ikhlas, K. Shirer et. al., Appl. Phys. Lett. 117 (2020).

Authors

• M. Ikhlas, K. Shirer^a, P.-Y. Yang^a, A. P. Mackenzie^a, C.W. Hicks^a, and S. Nakatsuji
• ^aMax Planck Institute for Chemical Physics of Solids