Topological Properties of τ-Type Organic Conductors
Osada Group
It is desirable that topological phases can be realized in organic molecular crystals with high designability. However, the search for topological states in organic crystals has met with some challenges. Generally, organic molecular crystals have too poor symmetry to protect topological states. The width of their tight-binding band is too narrow to cause the band inversion. Moreover, organic molecules consist of light elements with correspondingly small spin–orbit coupling (SOC). So far, only a few molecular crystals, such as a two-dimensional (2D) Dirac semimetal α-(BEDT-TTF)2I3 and a 3D nodal-line Dirac semimetal Pd(dddt)2, have been studied as topological materials in the field of organic conductors.
Here, we demonstrate that the conducting layer of τ-type organic layered conductor, τ-(EDO-S,S-DMEDT-TTF)2X1+y and τ-(P-S,S-DMEDT-TTF)2X1+y (X=AuBr2, I3, IBr2), is a 2D electron system with unique topological properties [1]. On each layer, donor molecules (EDO-S,S-DMEDT-TTF or P-S,S-DMEDT-TTF) form a square lattice, and anion molecules (X) are arranged on it with a checkerboard pattern as shown in Fig. 1(a). This lattice structure is a modification of Mielke's lattice, which is a typical flat band system, so that topological natures of Mielke's lattice are inherited. In addition, rather strong spin-orbit coupling (SOC) can be expected in τ-type conductors, although SOC is generally weak in organic materials. It results from the strong in-plane potential modulation generated by the inorganic anion X. Using a Kane-Mele type model, we discuss possible topological properties of the τ-type organic conductors.
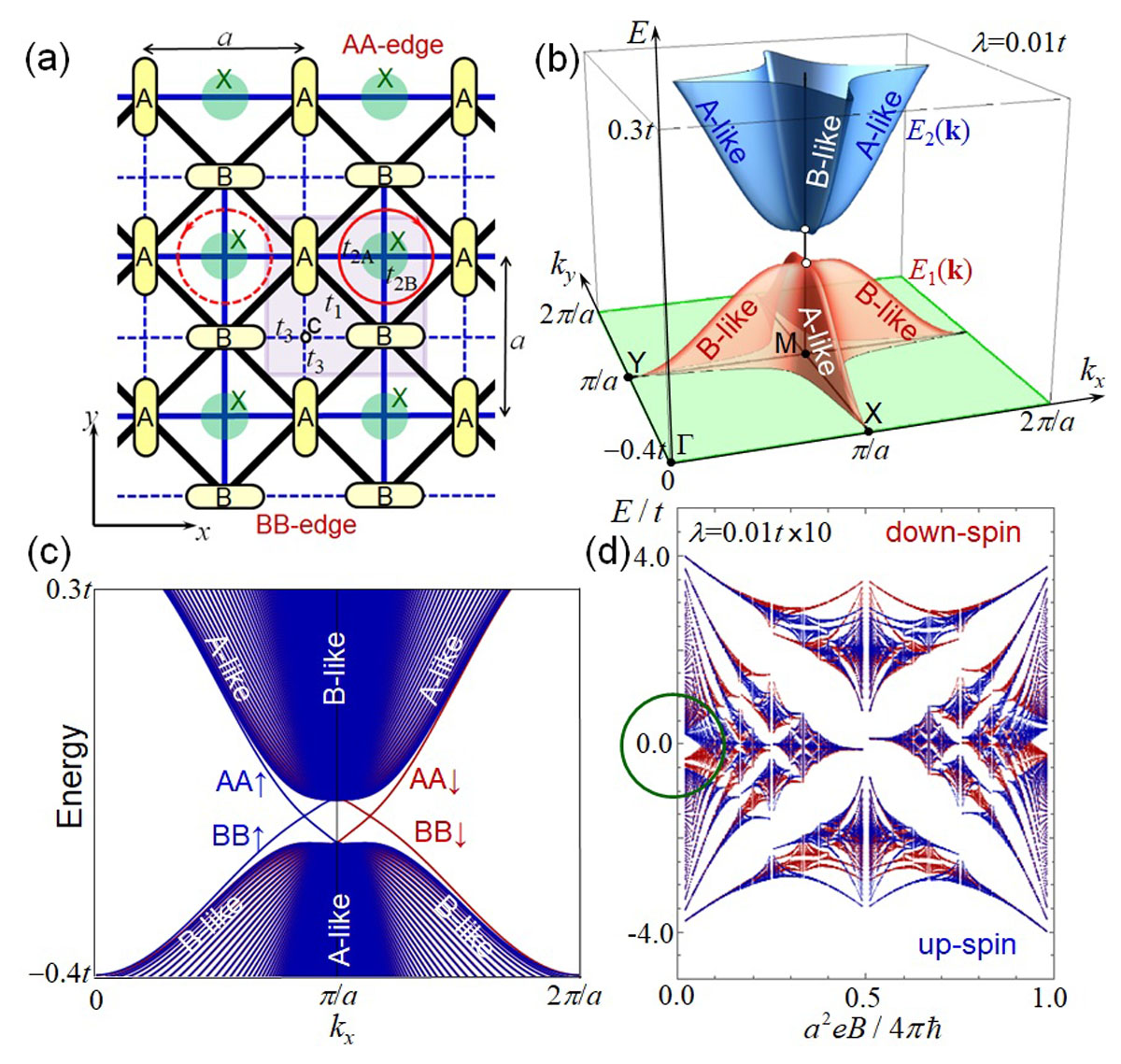
Fig. 1. (a) Schematics of a conducting layer of τ-type organic conductors. A and B indicate donor molecule sites, and X indicates anion sites. (b) Bulk band dispersion of τ-type conductors with finite spin-orbit coupling (SOC). A gap opens at the quadratic band contact point at M. (c) Energy dispersion of the system with finite width. Helical edge states along AA and BB edges appear in the gap. (d) Hofstadter butterfly (energy spectra as a function of magnetic field) of τ-type conductors. Blue and Red patterns correspond to up-spin and down-spin, respectively. The value of SOC is enlarged to see its effect easily.
In the absence of SOC, the conduction and valence bands with four-fold rotational symmetry show quadratic band touching. Since the Fermi level is located in the conduction band, the actual τ-type organic conductors (y = 0.75~0.875) have is a star-shaped electron Fermi surface. Under the in-plane uniaxial strain breaking the four-fold symmetry, the band contact point splits into a pair of Dirac cones. This is a kind of Lifshitz transition from a 2D Luttinger semimetal to a 2D Dirac semimetal.
Once the SOC becomes finite, a small gap opens at the band contact point as seen in Fig. 1(b). The product of the valence band parity values at symmetric point (time-reversal invariant momentums) is -1. This fact indicates that the gapped state is a topologically nontrivial insulator with band inversion. In fact, there exists a helical edge state characteristic to the quantum spin Hall insulator (Z2-topological insulator) along each edge as shown in Fig. 1(c). Therefore, the actual τ-type conductors could be regarded as heavily-doped topological insulators. Since they have finite spin-dependent Berry curvature at the Fermi level, finite spin Hall effect could appear although its experimental detection needs microfabrication of samples.
Because of finite spin-dependent orbital magnetic moment due to SOC, the Landau levels (LLs) have additional spin splitting to the Zeeman effect. Figure 1(d) shows the Hofstadter butterfly of the LLs for each spin subband. Since the Zeeman effect is not included in this figure, the difference of both spin levels indicates the orbital contribution to the spin splitting due to SOC. At the zero-field limit, we can see the Chern number below the SOC gap takes finite values of -1 or +1 depending on the spin. As actual τ-type conductors are doped up to 10% of the conduction band, the orbital contribution to the spin splitting is about several % of the Zeeman splitting, which is possible to detect experimentally in the Shubnikov-de Haas oscillations at low temperature and high magnetic fields.
References
- [1] T. Osada, J. Phys. Soc. Jpn. 88, 114707 (2019).
