Predicting and Understanding Structural Phase Transition of Solids from Finite-Temperature Phonon Calculations
T. Tadano and W. A. Saidi
The study of structural phase transition has been an active research subject in condensed matter physics and materials science because a variety of materials’ properties, including but not limited to transport, optical, and superconducting properties, often changes sensitively with the crystal structure. So far, first-principles calculations based on density functional theory (DFT) have been performed extensively for identifying (meta-)stable structures at T = 0 K. On the other hand, predicting finite-temperature structures based on DFT is still challenging because it requires a proper treatment of entropic effects of phonons and magnons. In particular, the vibrational entropy plays a central role in realizing structural phase transitions of nonmagnetic materials, including perovskite oxides such as BaTiO3. However, the conventional phonon calculation method based on the harmonic approximation (HA) often yields unstable phonon modes for high-temperature phases of phase change materials, which hinders an estimation of vibrational entropy.
To overcome the limitation of the conventional phonon calculation method, we have recently developed a new approach that is applicable to high-temperature phases [1]. Our method is based on the self-consistent phonon (SCP) theory, which incorporates the anharmonic renormalization of phonons at the mean-field level. We have so far employed the developed SCP scheme to compute finite-temperature phonons of cubic SrTiO3 [1], thermoelectric clathrate [2], and ScF3 [3], where we have obtained an excellent agreement with the experimental data. Also, it can be used to compute the vibrational free energy of solid whose structure is dynamically unstable within the HA, as has been demonstrated for ScF3 [3] and hydrogen-rich superconductors [4].
To further test and improve the prediction accuracy of our approach, we have recently applied the SCP method to an all-inorganic halide perovskite CsPbBr3, which has been actively studied in recent years as an efficient photovoltaic material. CsPbBr3 shows a successive structural phase transition with cooling from cubic α phase (Pm3¯m) to the tetragonal β phase (P4/mbm) at 403 K and then to the orthorhombic γ phase (Pnma) at 361 K. When the HA was used, we obtained unstable phonon modes for the high-temperature phases as shown in Fig. 1. These phonon modes involve a distortive motion of the bromine octahedra; therefore, these soft modes, particularly those at the M (1/2,1/2,0) point of the α phase and the Z (0,0,1/2) point of the β phase, may act as the soft modes of the structural phase transition. After including the effect of finite-temperature renormalization by the SCP theory, all phonon modes were stabilized, as shown by solid lines in Fig.1. After that, we calculated the vibrational free energies with including the effect of the quartic anharmonicity [3] and predicted the phase transition temperature (Tc) based on the calculated Helmholtz free energies. When we used the PBEsol exchange-correlational functional, the Tc values of the cubic-to-tetragonal and tetragonal-to-orthorhombic phase transitions were predicted as Tc ~ 280 K and Tc ~ 180 K, respectively, both of which underestimate the experimental results. To improve the prediction accuracy, we have further considered the higher-order correction to the vibrational free energy that originates from the cubic anharmonicity. Then, the Tc value of the cubic-to-tetragonal phase transition changed as Tc ~ 400 K, which shows better agreement with the experimental value.
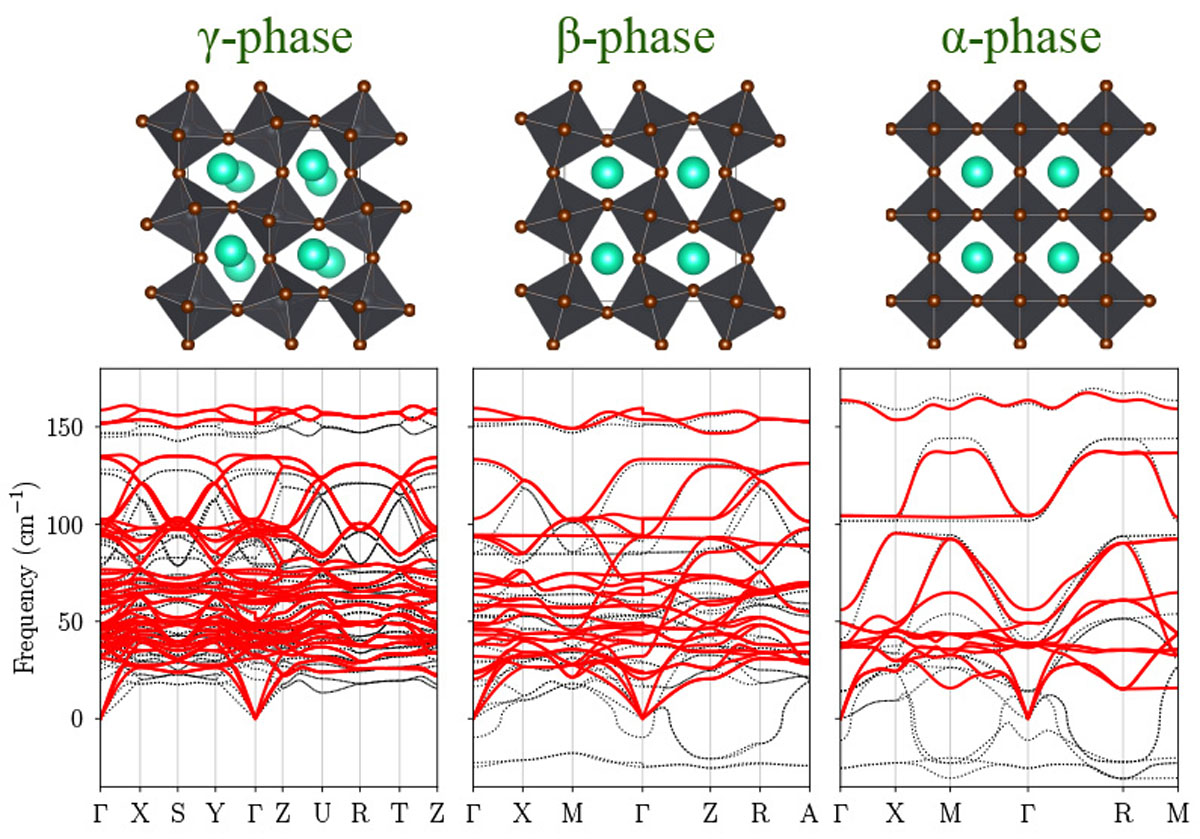
Fig. 1. (Top) Crystal structures of α, β, and γ phases of halide perovskite CsPbBr3. (Bottom) Phonon dispersion curves of three different phases of CsPbBr3 calculated within the harmonic approximation (dotted lines) and self-consistent phonon method at 500 K (solid lines). The unstable phonon modes in the high-temperature phases (β, γ) are stabilized by anharmonic renormalization at finite temperature.
We are also interested in how the structural phase transition affects thermal transport properties. To investigate this point quantitatively, we have calculated the lattice thermal conductivity of CsPbBr3 for the three different phases. To this end, we calculated the phonon lifetimes by considering the three-phonon scattering process on top of the SCP calculations. After that, the lattice thermal conductivity was estimated, where both of the particle-like transport and coherent transport terms were calculated following Ref. [5]. For all phases, the thermal conductivity values were smaller than 1 W/mK, indicating the strong lattice anharmonicity of CsPbBr3. We found that the lattice thermal conductivity of the high-temperature α phase was larger than those of the low-temperature phases due to the longer phonon lifetimes in the highly symmetric α phase, which can be attributed to the smaller scattering phase space of the three-phonon process. Interestingly, unlike the conventional semiconductors where most of the thermal transport is accounted for by the highly dispersive acoustic phonons, more than ~60% of the total thermal conductivity was carried by optical phonons above 30 cm-1 in CsPbBr3.
The computational results on CsPbBr3 again highlight the versatility and efficiency of the SCP theory for studying lattice dynamics in solids. While it is tempting to state that the SCP-based approaches are already reliable enough to make a quantitative prediction of structural phase transitions, many effects are yet to be investigated, including thermal expansion and choice of the exchange-correlation functionals. Investigating these effects on a Tc value would be an important future direction for our forthcoming studies.
References
- [1] T. Tadano and S. Tsuneyuki, Phys. Rev. B 92, 054301 (2015); J. Phys. Soc. Jpn. 87, 041015 (2018); J. Ceram. Soc. Jpn. 127, 404 (2019).
- [2] T. Tadano and S. Tsuneyuki, Phys. Rev. Lett. 120, 105901 (2018).
- [3] Y. Oba, T. Tadano, R. Akashi, and S. Tsuneyuki, Phys. Rev. Materials 3, 033601 (2019).
- [4] I. Errea, F. Belli, L. Monacelli, A. Sanna, T. Koretsune, T. Tadano, R. Bianco, M. Calandra, R. Arita, F. Mauri, and J. A. Flores-Livas, Nature 578, 66 (2020).
- [5] M. Simoncelli, N. Marzari, and F. Mauri, Nature Phys. 8, 809 (2019).
