Fluctuation-Induced First-Order Transition and Tricritical Point in a Cubic Chiral Magnet EuPtSi
Sakakibara Group
The cubic chiral compound EuPtSi (space group P213) helimagneitcally orders at TN=4.0 K with the propagation vector q1*=(0.2, 0.3, 0.04). There has been growing interest in this compound because a skyrmion lattice phase with a triple-q structure emerges in a magnetic field applied along the [111] direction [1,2]. One of the intriguing features of this compound is that the transition at TN is of first order [1-3]. We studied the helimagnetic transition on a single crystal of EuPtSi by means of high-precision magnetization measurements, and found that the transition, which is of first order at low fields, becomes of second order at high fields, and there exists a tricritical point (TCP) in the phase diagram [4].
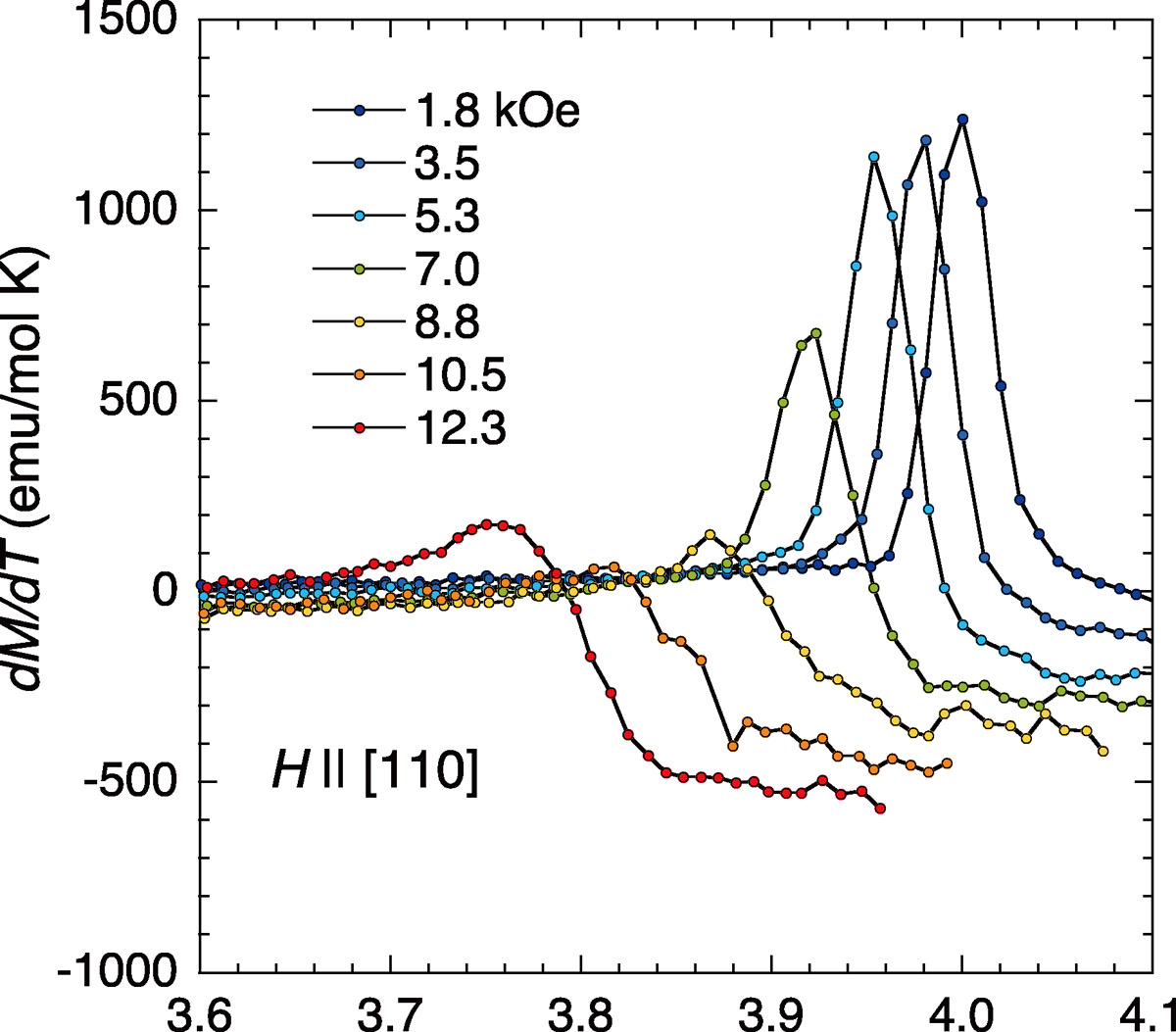
Figure 1 shows the temperature derivative of the magnetization, dM/dT, in magnetic fields H applied along the [110] direction. At H = 1.8 kOe, the first-order transition (FOT) is characterized by a sharp peak in dM/dT at T = 4.0 K. By increasing H, TN(H) defined by the peak position in dM/dT moves to the lower temperature side with a decrease in the peak amplitude. Above H = 8.8 kOe, the shape of dM/dT dramatically changes and excibits a step function like jump at TN(H), implying that the transition becomes of second order above 8.8 kOe.
In order to construct the phase boundary between the paramagnetic and the ordered states, we show in Fig. 2 the color contour mapping of the dM/dT data for H||[110]. The bright line in the low-field region indicates the FOT boundary, and the dashed line in the high-field region denotes the second-order one. In between there is a TCP as indicated in the figure. A similar crossover of the transition has also been observed for [111] and [100] directions [4].
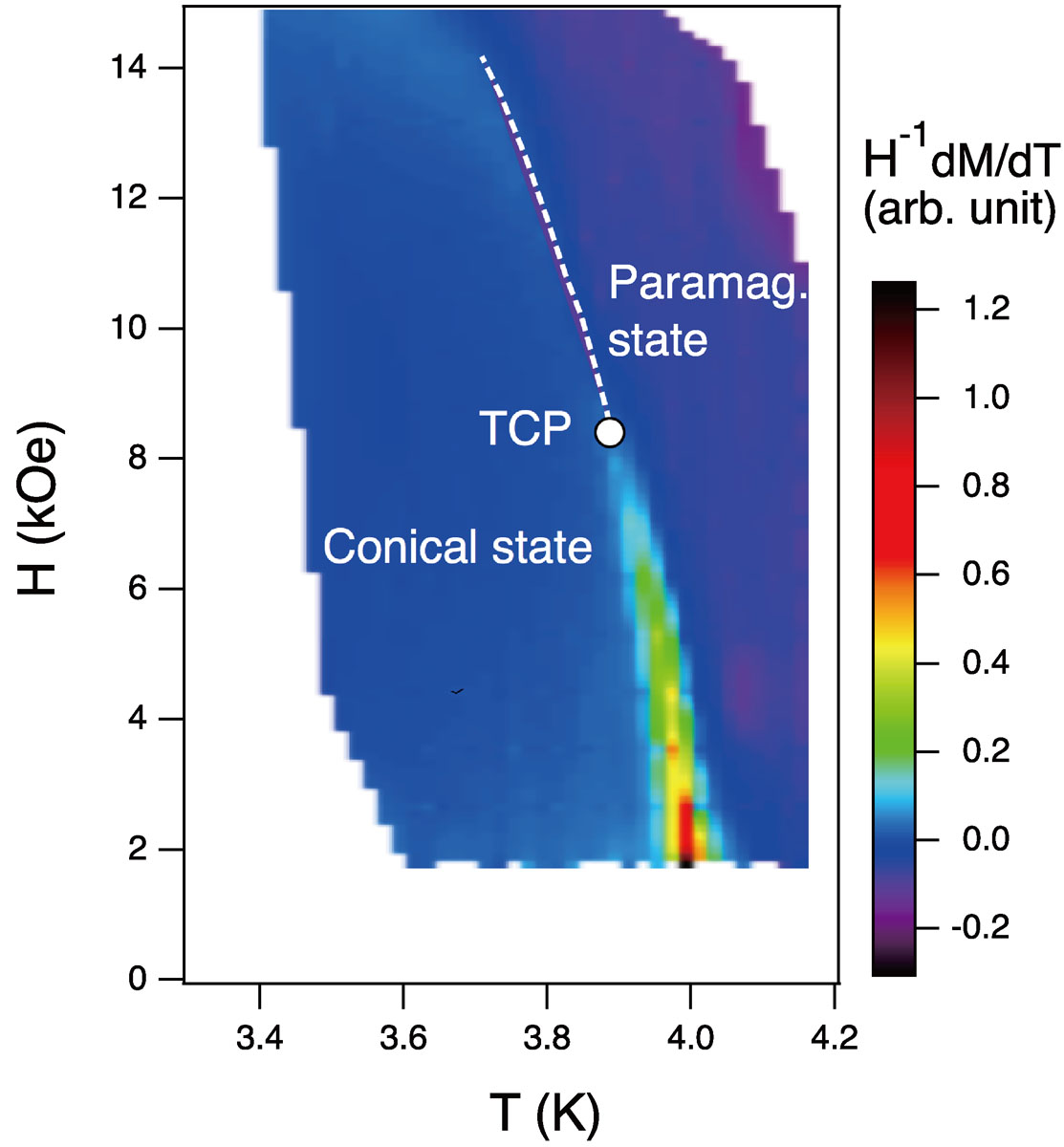
Fig. 2. Phase boundary between the paramagnetic and the single-q helical (conical) states of EuPtSi, constructed by colour contour mapping of the dM/dT data with H||[110]. The bright line in low fields indicates the first-order boundary, whereas the dashed line shows the second-order one. TCP denotes the position of the tricritical point.
In systems described by order parameters with n>4 components, a usual second-order phase transition is avoided due to interactions among critical fluctuations of the order parameters [5]. FOT then takes place when the correlation length exceeds a certain limit, where a discontinuous phase transition occurs to a state energetically favorable. This fluctuation-induced FOT takes place even for systems in which the mean-field theory predicts second-order phase transitions, and the actual transition temperature is suppressed much below the mean-field transition temperature. In EuPtSi, the lattice-symmetry operations on q1* yields 12 distinct propagation vectors, which is large enough in number to drive the transition to be first order. Applying a magnetic field reduces the symmetry of the system, and the number of components of the order parameter is effectively decreased, leading to a second-order phase transition. The presence of TCP in the phase diagram in Fig. 2 supports this scenario of a fluctuation-induced FOT in EuPtSi. This situation is favorable for the occurrence of multi-q orders such as the skyrmion lattice phase, since they need to be stabilized against a single-q helical (or a conical) phase.
References
- [1] M. Kakihana et al., J. Phys. Soc. Jpn. 87, 023701 (2018).
- [2] K. Kaneko et al., J. Phys. Soc. Jpn. 88, 013702 (2019).
- [3] D.G. Franco et al., Phys. Rev. B 96, 014401, (2017).
- [4] T. Sakakibara et al., J. Phys. Soc. Jpn. 88, 093701 (2019).
- [5] P. Bak, S. Krinsky and D. Mukamel, Phys. Rev. Lett. 36, 52 (1976).