In a number of strongly correlated electron systems, the electronic nematic (EN) state characterized by the lacking of the C₄^±-rotational operations has been focused because the EN contribution to superconductivity and other exotic phenomena have been proposed. Recently, the field-induced EN phase above 30 T has been proposed in the D_4h¹ tetragonal compound of CeRhIn5 [1,2], which was well known as a pressure-induced heavy-fermion superconductor.

To investigate the active representation and the order parameter of the field-induced EN phase, we performed an ultrasonic measurement for CeRhIn₅ in pulsed magnetic fields up to 56 T [3]. The ultrasound technique is a powerful tool to determine the active representation of a phase transition related to the crystal symmetry breaking because sound waves can induce the symmetry strain belonging to the irreducible representation (IR) of the space group. Furthermore, we can propose the electric quadrupole as an order parameter of the crystal symmetry breaking and the EN state in terms of the electric quadrupole-strain interaction, which is based on the selection rule of group theory.

To identify the active representation of the symmetry breaking at the EN state, we measured all the elastic constants of CeRhIn₅ that can be detected in the tetragonal system. As shown in Fig. 1, the transverse elastic constant C_T = (C₁₁ − C₁₂)/2 with the B_1g IR of D_4h shows the anomaly at B_IM = 28.5 T at 1.4 K and 2.1 K. This B_IM is consistent with the previous studies [1, 2]. While C_T shows an anomaly, other elastic constants, which can identify the symmetry breaking of B_2g and E_g IR, do not exhibit anomaly at B_IM. Therefore, our ultrasonic measurements demonstrate the B_1g-type crystal symmetry breaking. Furthermore, the electronic degree of freedom with the B_1g IR, namely the electric quadrupole O_{x² − y²} ∝ (x² − y²)/r², can be the order parameter of the EN state. This symmetry breaking is attributed by the electric quadrupole-strain coupling written as H_QS = −g_{x² − y²} O_{x² − y²} ε_{x² − y²}.

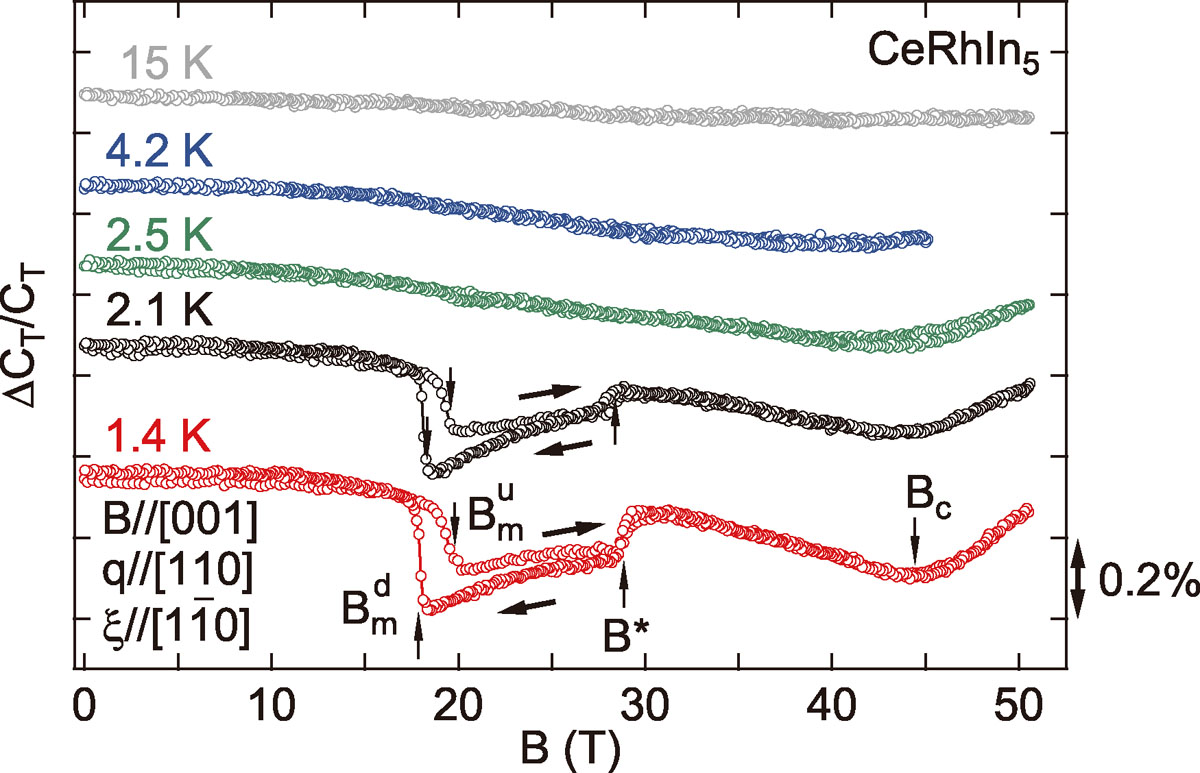
Fig. 1. Magnetic field dependence of the transverse elastic constant ΔC_T/C_T at several temperatures for B//[001]. The vertical arrows indicate the metamagnetic transition field B_m^u(d) for field up(down) sweep, the EN transition field B^*, and the critical field B_c. The right and left arrows show hysteresis direction. The propagation direction q and polarization direction of ultrasound are indicated.

We show the schematic view of the B_1g-type ferroic electric quadrupole ordering and crystal symmetry breaking in Fig. 2. The square lattice of CeRhIn5 with the tetragonal crystal structure of D_4h¹ is drawn in Fig. 2(a). In the field-induced EN state, the electric quadrupole O_{x² − y²} appears on the Ce site. The lattice changes from the square of the tetragonal structure to the rectangle of orthorhombic one due to the quadrupole-strain coupling HQS accompanying the lattice distortion ε_{x² − y²} = ε_xx − ε_yy. A maximal nonisomorphic orthogonal subgroup D_2h¹ is an appropriate space-group for this symmetry lowering from D_4h¹.

Furthermore, we found the acoustic de Haas-van Alphen (AdHvA) oscillation in C_T with the frequency 690 T, which has not been observed experimentally. On the other hand, the theoretical study treating 4f electrons as itinerant has shown a hole Fermi surface with the frequency ~ 690 T [4]. Thus, we proposed the origin of the AdHvA oscillation in terms of the quadrupole-strain coupling in the k-space based on the deformation potential theory [5].

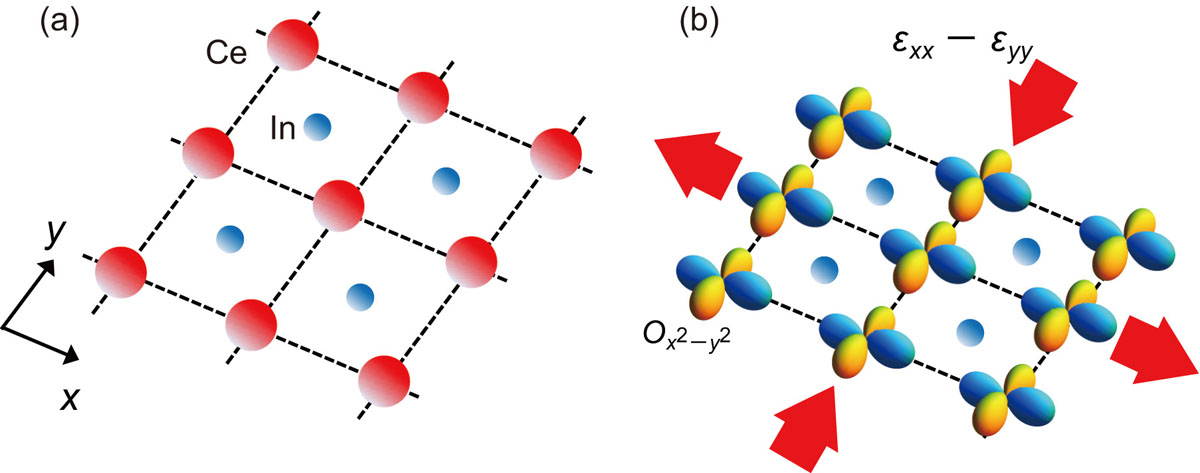
Fig. 2. Schematic view of the B_1g-type quadrupole ordering and crystal symmetry breaking. (a) Crystal structure in the xy plane of CeRhIn₅ in the normal phase. (b) High-field symmetry breaking state of CeRhIn₅. The red arrows indicate the deformation direction of the crystal lattice due to the strain ε_{x² - y²} = ε_xx - ε_yy.

We also discussed the quantum state possessing the electric quadrupole. The delocalization of 4f electrons and the in-plane type p-f hybridization are candidate interactions constructing the quantum state in high fields.

References

• [1] P. J. Moll et al., Nat. Commun. 6, 6663 (2015).
• [2] F. Ronning et al., Nature (London) 548, 313 (2017).
• [3] R. Kurihara et al., Phys. Rev. B 101, 115125 (2020).
• [4] D. Hall et al., Phys. Rev. B 64, 064506 (2001).
• [5] M. Kataoka and T. Goto, J. Phys. Soc. Jpn. 62, 4352 (1993).

Authors

• R. Kurihara, A. Miyake, M. Tokunaga, Y. Hirose^a, and R. Settai^a
• ^aNiigata University