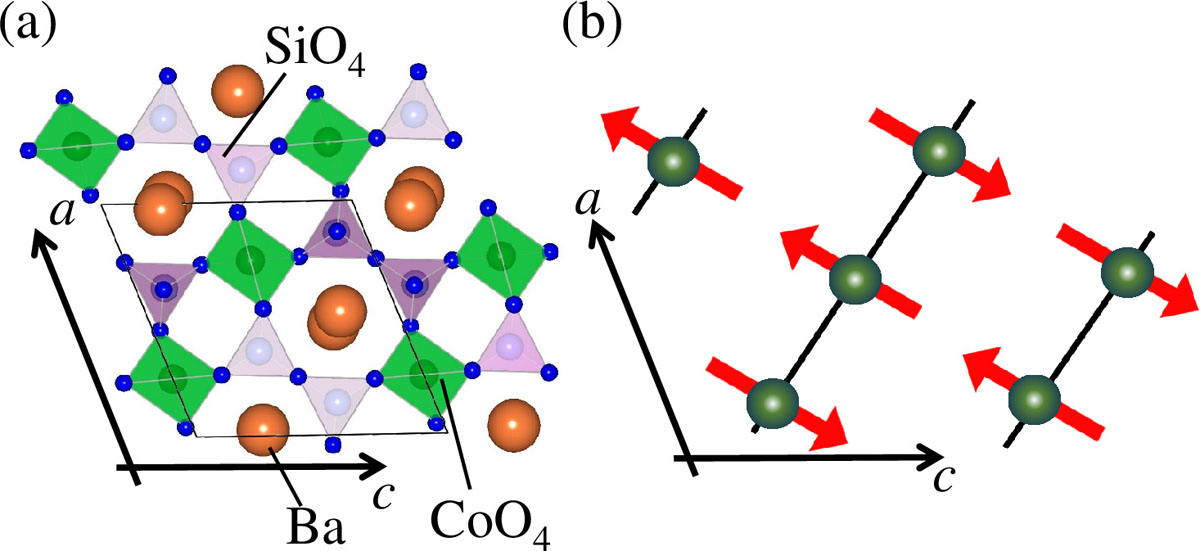
The relationship between magnetism and dielectricity has been extensively studied. In the multiferroics, the ferroelectrics with the cycloidal and proper-screw magnetic structures are explained by the spin-current mechanism and the spin-dependent d–p hybridization mechanism, respectively [1,2]. On the other hand, the multiferroic property has been reported even on a collinear antiferromagnet. One of the maultiferroics with the collinear magnetic structure is an antiferromagnet Ba₂CoGe₂O₇. Ba₂CoGe₂O₇ with the Co-square lattice shows multiferroic properties, and the local electric polarization of CoO₄ tetrahedra is explained by the spin-dependent d-p hybridization mechanism [3,4]. In contrast, the anomaly of the dielectric constant in similar material Ba₂CoSi₂O₇ is not observed at the antiferromagnetic transition temperature T_N =6 K [5]. Ba₂CoSi₂O₇ has a distorted crystal structure formed by CoO4 and SiO₄ networks, as shown in Fig. 1(a), and two kinds of Co-Co bonds exist within the b-plane. In order to clarify the magnetic model of Ba₂CoSi₂O₇, the magnetization and neutron scattering measurements have been performed.

Fig. 1. (a) Crystal structure of Ba₂CoSi₂O₇. (b) Schematic magnetic structure of Ba₂CoSi₂O₇.

In the neutron powder diffraction measurement using the high-resolution powder diffractometer ECHIDNA installed at OPAL, ANSTO, Australia, the magnetic reflections indexed by the propagation vector (1/2, 1/2, 1/2) was observed below T_N = 6 K. By analyzing the powder neutron profile, we found that a collinear antiferromagnetic structure shown in Fig. 1(b) was realized below T_N = 6 K. The magnetic moments with the easy axis along the [10-1] form an antiferromagnetic arrangement along [101] and a ferromagnetic arrangement along [10-1]. In the spin-dependent d-p hybridization mechanism, the local electric polarization of the CoO₄ tetrahedron is almost zero with the magnetic moment along [10-1]. This is consistent with the dielectric property where the temperature dependence of the dielectric constant has no anomaly at T_N = 6 K.

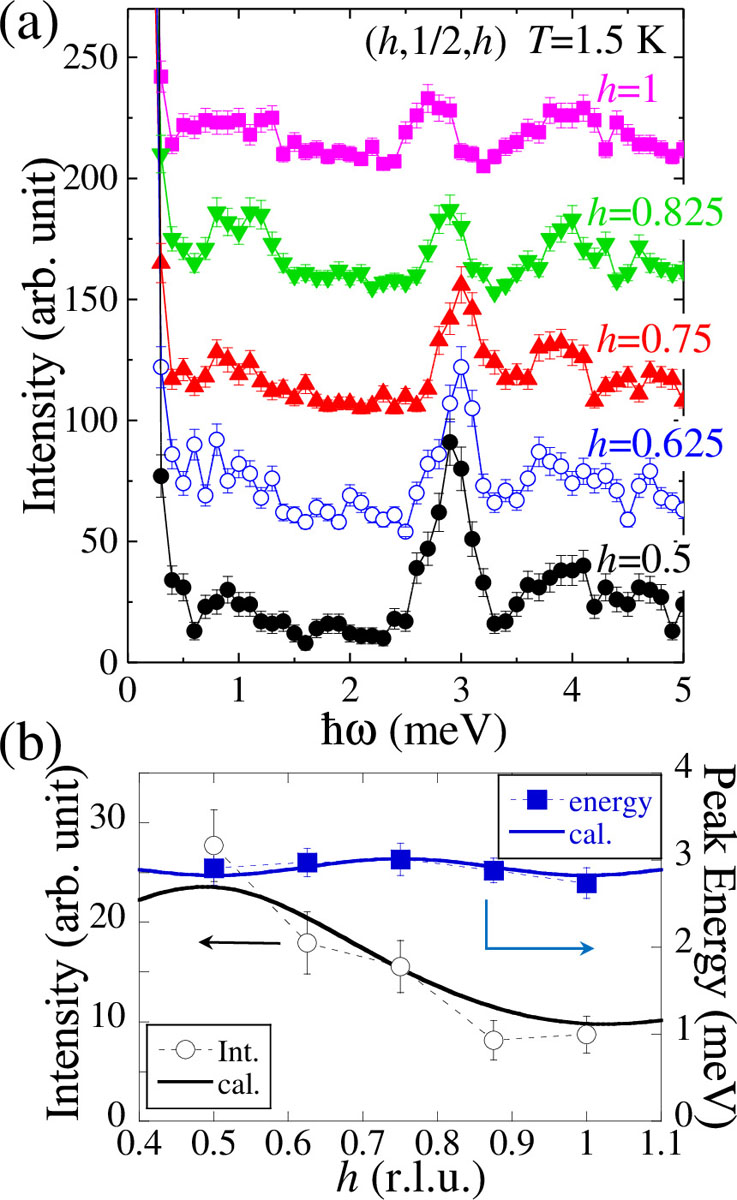
We have also measured the Q-dependencies of the magnetic excitations along the b^*, [10-1], and [101] directions at 1.5 K to clarify the magnetic correlation of Ba₂CoSi₂O₇ by using a cold-neutron triple-axis spectrometer (CTAX) installed at HFIR, ORNL, USA. Figure 2(a) shows the constant-Q scan profiles measured at (h, 1/2, h). Figure 2(b) shows the h-dependence of integrated intensities and peak energies obtained by Gaussian fitting of the constant-Q profiles at (h, 1/2, h), which corresponds to the Q-dependence along the [101] direction. The excitation observed at ħw = 2.9 meV is almost dispersionless, but the integrated intensity exhibits a clear modulation along the [101] direction. In the measurements along the b^* and [10-1] directions, on the other hand, both the neutron intensity and peak energy show less change. (not shown)

Fig. 2. (a) Constant-Q scans at (h, 1/2, h) measured at 1.5 K. Data are shifted by vertical offsets. (b) Integrated intensities and the peak energies at (h, 1/2, h). Solid lines are the calculated values with the classical spin-wave theory.

We analyzed the magnetic excitation by using the spin Hamiltonian in order to clarify the magnetic model including the magnetic interaction in Ba₂CoSi₂O₇. To explain the observed magnetic excitation, we consider the one-dimensional antiferromagnet in which the antiferromagnetic chain is along the [101] direction. We performed the calculations of the neutron intensity and the dispersion energy for both the easy-axis and Ising-like antiferromagnet models; two models cannot be distinguished in the classical spin-wave theory. The magnetic dispersion relation shown in Fig. 2(b) is reproduced by the one-dimensional antiferromagnet model, as shown by solid curves.

Our results of the neutron scattering suggest that the Ba₂CoSi₂O₇ is the one-dimensional antiferromagnet with the easy-axis spin anisotropy or the Ising-like spin. On the other hand, Ba₂CoGe₂O₇ with the tetragonal structure is two-dimensional easy-plane antiferromagnet. The neutron results suggest that the crystal structure affects both the magnetic interaction dimensionality and anisotropy in åkermanite-type materials.

References

• [1] T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima, and Y. Tokura. Nature 426, 55 (2003).
• [2] S. Seki, Y. Onose, and Y. Tokura. Phys. Rev. Lett. 101 067204 (2008).
• [3] H. Murakawa, Y. Onose, S. Miyahara, N. Furukawa, and Y. Tokura. Phys. Rev. Lett. 105, 137202 (2010).
• [4] M. Soda, M. Matsumoto, M. Månsson, S. Ohira-Kawamura, K. Nakajima, R. Shiina, and T. Masuda, Phys. Rev. Lett. 112, 127205 (2014).
• [5] M. Akaki, J. Tozawa, D. Akahoshi, and H. Kuwahara, J. Phys.: Conf. Ser. 150, 042001 (2009).

Authors

• M. Soda^a, T. Hong^b, M. Avdeev^c, H. Yoshizawa^a, T. Masuda, and H. Kawano-Furukawa^a,^d
• ^aRIKEN
• ^bORNL
• ^cANSTO
• ^dOchanomizu University