Novel Excitations near Quantum Criticality in Geometrically Frustrated Antiferromagnet CsFeCl3
Masuda Group
For understanding condensed matter, the investigation of the collective excitation in low energy range is indispensable. According to the quantum field theory, the excitation in the system with spontaneously symmetry broking is characterized by phase and amplitude fluctuations of order parameters. The former is known as the Nambu-Goldstone (NG) mode, and the latter is called as the amplitude mode. Even though these modes are usually separated, they are hybridized under some conditions, and interesting phenomena are induced; for example in a crystal lattice system, acoustic phonon (NG mode) and optical phonon (amplitude mode) are hybridized through anharmonic terms in a thermoelectric material PbTe, which renormalizes the phonon spectrum and leads to low thermal conductivity and high figure of merit in thermoelectric property [1]. Such a hybridization effect could exist in other types of elementary excitations, however, no research has been reported to our knowledge partially because longitudinal mode itself is not trivial.
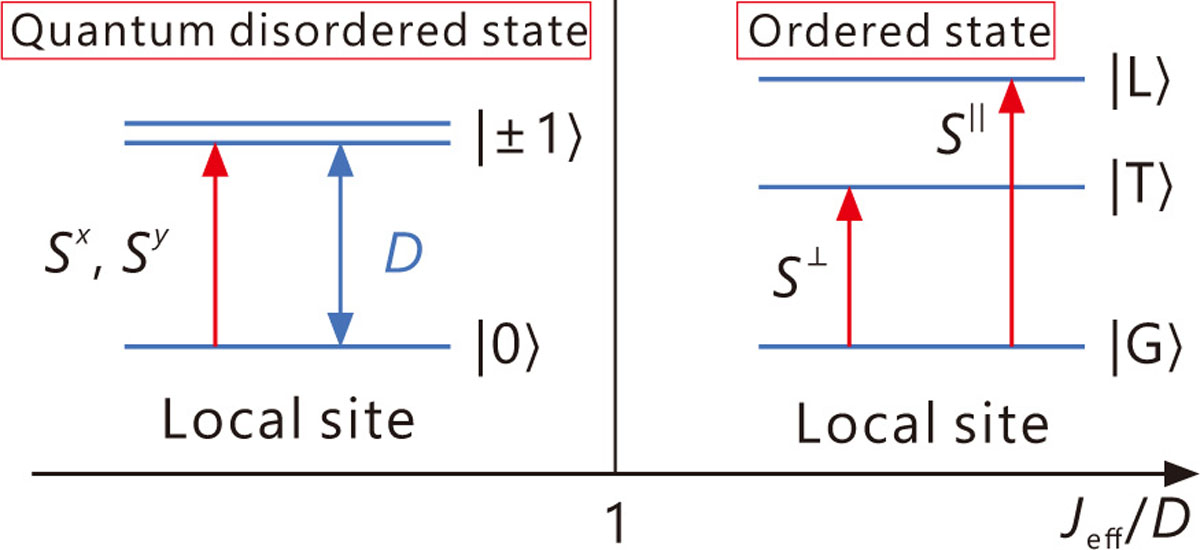
Spin S = 1 easy-plane antiferromagnet is one of the prototypical quantum spin systems that allows to explore the quantum phase transition (QPT) [2]. When the anisotropy D is large, the ground state is a quantum disordered (QD) singlet as shown in Fig. 1 left panel. When D is small and the exchange interaction is large, the ground state is magnetically long-range ordered state. A remarkable feature in the renormalized energy scheme in Fig. 1 right panel is that the second excited state can be excited only by the longitudinal component of spin operator S||, meaning that the longitudinal mode is allowed in the system. Because the geometrical frustration in magnets could induce the hybridization of the transverse (T) and longitudinal (L) modes, spin S = 1 easy-plane antiferromagnet having geometrically frustrated lattice is the best playground for the research of hybridized modes in magnetic material.
Fig. 1. Schematic diagram of the S = 1 easy-plane antiferromagnet. In the ordered state, the doublet excited states |±1> splits into |L> and |T>. Here, the former and latter have longitudinal and transverse fluctuations, respectively.
CsFeCl3 is the S = 1 easy-plane triangular antiferromagnet. The inelastic neutron scattering (INS) study at ambient pressure revealed that the ferromagnetic chains along the crystallographic c axis are antiferromagnetically coupled in the ab plane [3]. The ground state is the QD state because of large single-ion anisotropy. The magnetic susceptibility measurement under pressures exhibited a pressure-induced magnetic order above a critical pressure of about 0.9 GPa [4]. Owing to the strong easy-plane anisotropy, the ordered moment aligns in the ab plane; the neutron diffraction evidenced the noncollinear 120° structure in the LRO phase [5]. CsFeCl3 is, thus, a promising host for the pressure-induced QPT in the geometrically frustrated lattice. In 2019 our group reported a new hybridization of the phase and amplitude fluctuations of the order parameter near QCP in CsFeCl3 [6].
The INS spectrum measured at 0.0 GPa by using chopper spectrometer in Fig. 2A exhibits a single dispersive excitation with the energy gap of 0.6 meV at the wave vectors q = (-k, 2k, 0) for k = 1/3 and 2/3. The energy gap at 0.3 GPa in Fig. 2B becomes softened when approaching the ordered state. A qualitatively different spectrum is observed in the ordered state at 1.4 GP in Fig. 2C. A well-defined gapless excitation emerges at k = 1/3 and 2/3 and another dispersive excitation are observed in the higher energy range. The INS spectra were collected also by using a triple-axis spectrometer in order to cover wide ħω – q range, and the extracted peak energies are overplotted by open symbols in Figs 2A-2C. At 1.4 GPa, the spectral lineshape at k = 5/6 was reproduced by double Lorentzians with broad widths which is reflected by large errorbars. The dispersion relations calculated by the extended spin-wave theory (ESW) [7] are indicated by the solid yellow curves. The calculation is consistent with the experiment both in the QD and LRO phases.
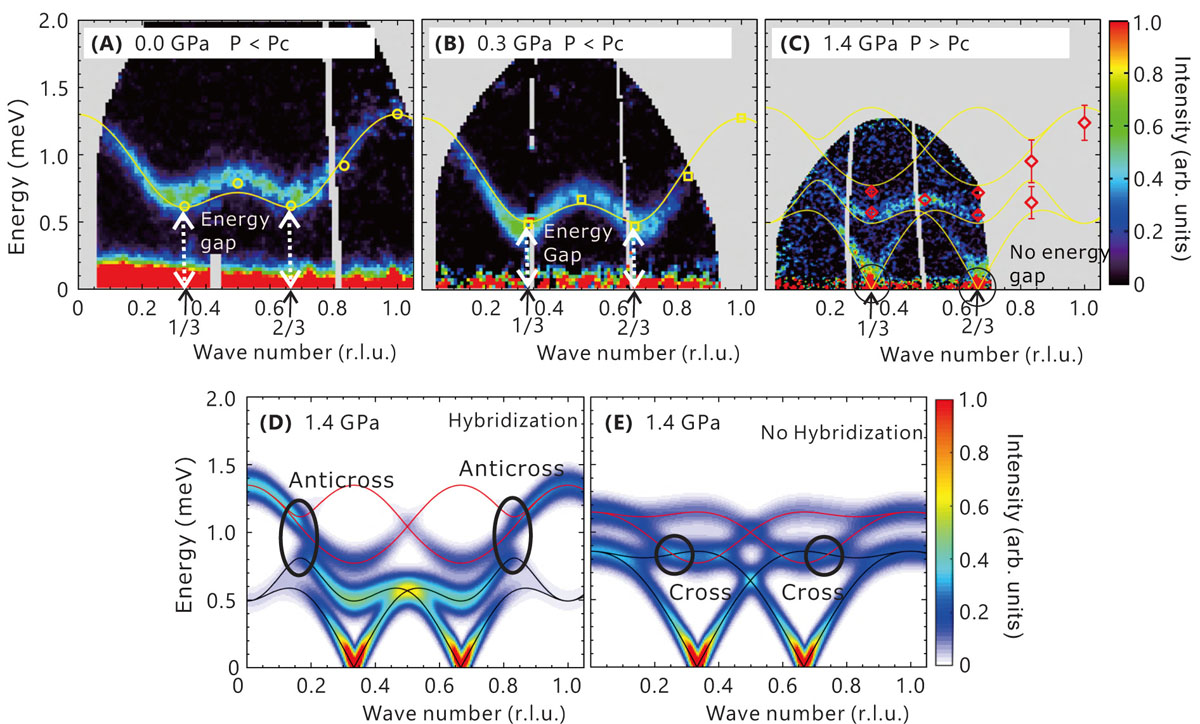
Fig. 2. Inelastic neutron scattering spectra. The spectra obtained at a chopper spectrometer under (A) 0.0 GPa at 6 K, (B) 0.3 GPa at 2.7 K and (C) 1.4 GPa at 0.9 K sliced by the energy transfer - wave vector (ħω – q) plane for q = (-k, 2k, 0). The yellow circles, squares, and red diamonds are the peak positions of the excitations obtained from the constant-q scans using a triple-axis spectrometer. The solid yellow curves are the dispersions calculated by ESW. Calculated neutron cross-section by the ESW under (D) 1.4 GPa at 0 K. Calculated neutron cross-section in the absence of the off-diagonal elements under (E) 1.4 GPa at 0 K. The black and red solid curves in (D) and (E) are gapless and gapped modes, respectively.
In ESW calculation one can notice that noncollinearity of the magnetic structure makes off-diagonal elements in the Hamiltonian nonzero, leading to the hybridization of L and T modes in one-magnon process. To understand the effects of LT-hybridization, we demonstrate the INS spectra after dropping the off-diagonal element. The results are shown in Figs. 2E, where the black-gapless (red-gapped) modes are pure transverse (longitudinal) modes in this case. The result is inconsistent with the experiment in Fig. 2C. When LT-hybridization is taken into account, the off-diagonal elements lead to anticross of the modes at k~ 5/6 in Fig. 2D, and novel magnetic excitations are formed; both gapless and gapped modes are accompanied by strong longitudinal and transverse fluctuations. The result is consistent with the experiment, and, thus, the LT-hybridization plays an important role in magnon dynamics in noncollinear magnet near QCP.
Since the newly found excitation exists in a noncollinear spin structure, the search of the excitation in different types of noncollinear structures such as cycloidal structure, all-in-all-out structure, and skyrmion lattice would be interesting topics. The search of the hybridized mode in other systems including charge density wave, spin density wave, and ultra-cold atoms would be important. Finally, the effect of hybridization to the lifetime of the magnon and other elementary excitations would be also interesting.
References
- [1] O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M. H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden, and B. C. Sales, Nat. Mat. 10, 614 (2011).
- [2] M. Matsumoto and M. Koga, J. Phys. Soc. Jpn. 76, 073709 (2007).
- [3] H. Yoshizawa,W. Kozukue, and K. Hirakawa, J. Phys. Soc. Jpn. 49, 144 (1980).
- [4] N. Kurita and H. Tanaka, Phys. Rev. B 94, 104409 (2016).
- [5] S. Hayashida, O. Zaharko, N. Kurita, H. Tanaka, M. Hagihala, M. Soda, S. Itoh, Y. Uwatoko, and T. Masuda, Phys. Rev. B 97, 140405 (2018).
- [6] S. Hayashida, M. Matsumoto, M. Hagihala, N. Kurita, H. Tanaka, S. Itoh, T. Hong, M. Soda, Y. Uwatoko, and T. Masuda, Sci. Adv. 5, eaaw5639 (2019).
- [7] R. Shiina, H. Shiba, P. Thalmeier, A. Takahashi, and O. Sakai, J. Phys. Soc. Jpn. 72, 1216 (2003).