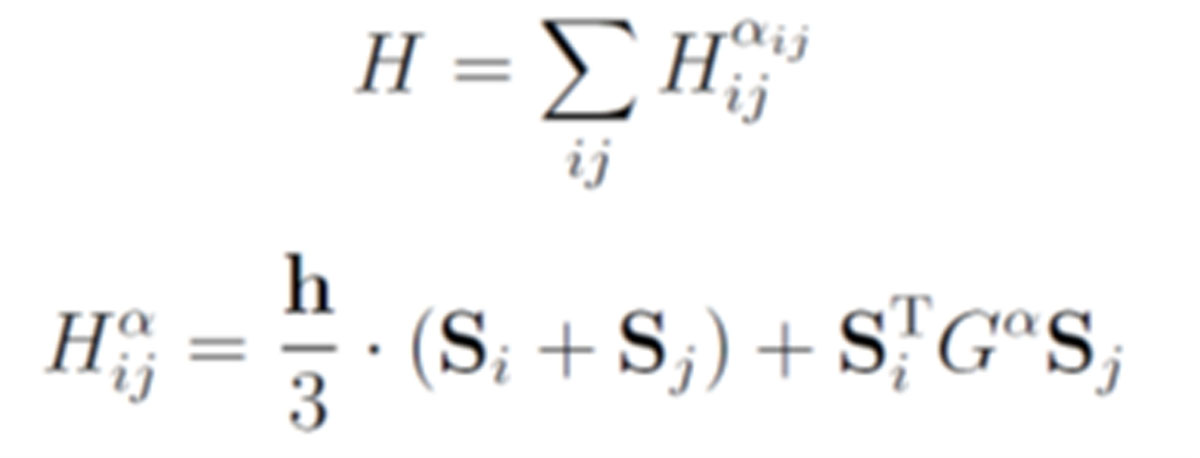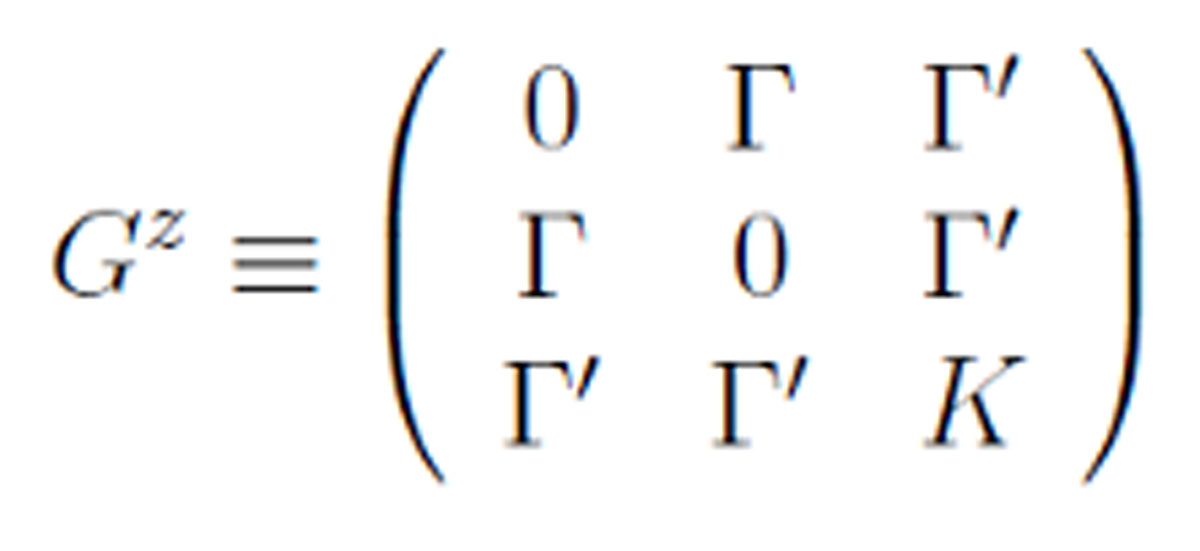Magnetic Field Induced Quantum Phases in a Tensor Network Study of Kitaev Magnets
Kawashima Group
Tensor network (TN) is a useful concept in various fields, not only in the condensed matter theory, but also in data science and machine learning. Even in the condensed matter theory alone, the application of the TN concept is multi-fold. In variational principles calculation, the TN is used as a new type of variational wave function. In the real-space renormalization group (RG) theory, it serves as a natural representation of a renormalized system. In the pure mathematical physics, it is used as a new language for discussing the topological nature of the quantum states.
In our previous study [Lee, Kaneko, Okubo and Kawashima: Phys. Rev. Lett. 123, 087203 (2019)], we studied the Kitaev model by the TN representation. We proposed a new wave function that is extremely simple in the TN representation but still shares many essential properties with the ground state of the Kitaev model, such as the quasi-long-range correlation, the short-range magnetic correlation, the flux-free property, the Z2 gauge structure, and the 2D Ising universality. We call this state the "loop gas state" because of its mathematical equivalence to the loop gas model, one of the standard and solvable statistical physical models. We showed that the loop gas state is adiabatically connected to the ground state of the Kitaev model, indicating a similar role to the AKLT state for the S = 1 AFH chain.
We then extended our method to several other models: S = 1 Kitaev model, and Kitaev-Gamma model. In this study, we studied field-induced quantum phases in the theoretical model of a real candidate material of Kitaev magnets, i.e., α-RuCl3. For this compound, there was an experimental discovery of the half quantized thermal Hall conductivity, which initiated a series of theoretical investigations aiming at finding a concrete connection between the observed quantum phenomena and the theoretical developments of the Kitaev spin liquid. Our TN calculation suggested that a field-induced phase appears between the low field zig-zag magnetic order and the high field polarized state. We found that the chiral Kitaev spin liquid occupies an area in the phase diagram, smaller than predicted by other groups.
Specifically, we studied the K-Γ-Γ' model on the honeycomb lattice represented by the following Hamiltonian,
where αij = x,y,z depending on the direction of the bond (ij). The magnetic field is along the [111] direction. The matrix Gα characterizes the two-body anisotropic interaction, e.g, for α = z,
The matrices for other directions are defined similarly.
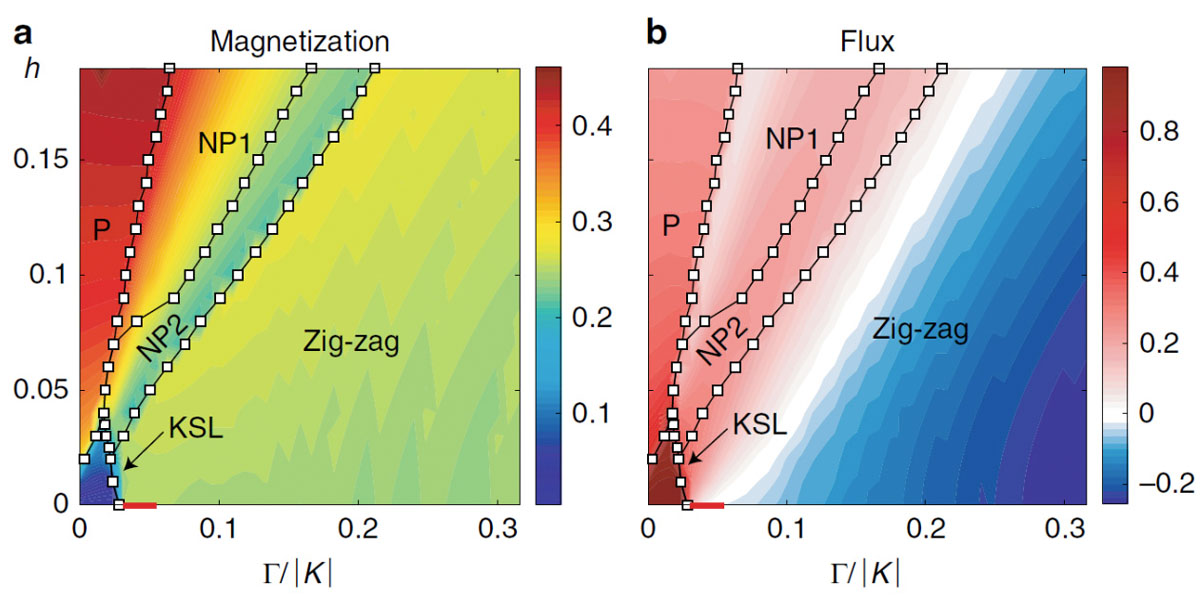
In Fig. 1, the obtained phase diagram is presented. The KSL ground state survives only in a small corner of the phase diagram. It disagrees with the previous results obtained by 24-site exact diagonalization and DMRG studies, which suggested a largely extended KSL phase. The discrepancy may imply the importance of the thermodynamic limit. The tensor network method provides us results for infinite system in contrast to the methods used in the previous ones. At zero field, there is a transition from KSL to a FM (ferromagnetic) phase where spins are aligned in the [111] direction. However, with a very weak magnetic field (h = 0.005), the FM phase disappears, and a direct phase transition from KSL to ZZ (zigzag magnetic ordered) occurs. With increasing the magnetic field, the transition from KSL to the P (polarized) phase occurs at a finite h, where spins start aligning in the [111]-direction.
Fig. 1. (a) The magnetization and (b) the flux expectation value of the K-Γ-Γ' model at Γ'= - 0.03. Here "KSL" stands for the chiral Kitaev spin liquid, "P" for a spin-polarized phase, and "NP1" and "NP2" for nematic paramagnet phase. The red solid line at h = 0 denotes a ferromagnetic phase.
Apart from the KSL phase, we discovered two non-magnetic states, NP1 and NP2. These phases are characterized by spontaneously-broken 120-degree-lattice-rotational symmetry. When the magnetic field is tilted so that the lattice-rotational symmetry is broken by the Hamiltonian, we found that the phase transition between the KSL and NP2 is continuous in spite that both phases have the same symmetry. This may indicate the non-trivial topological nature of the NP2 phase, which should be clarified in the future study.
References
- [1] H.-Y. Lee, R. Kaneko, L. E. Chern, T. Okubo, Y. Yamaji, N. Kawashima, and Y. B. Kim, Nature Communications 11, 1639 (2020)