The series of Pr-based cubic compounds PrT₂X₂₀ (T = Ir, Rh, X = Zn; T = V, Ti, X = Al) has been actively studied recently to explore novel phenomena caused by multipoles of 4f electrons because the non-Kramers Γ₃ doublet ground states in the crystalline electric field (CEF) has active quadrupole (O_Z = 3z²-r² and O_X = √3(x²-y²)) and an octupole (T_XYZ = xyz) moments but no magnetic dipole moment [1]. Among this series, PrTi₂Al₂₀ shows the highest transition temperature of 2 K into a simple ferro-ordered state of O_Z quadrupole moment.

We have performed ²⁷Ai-NMR and magnetization measurements on high quality single crystals of PrTi₂Al₂₀ and unexpectedly observed discontinuous switching of quadrupole order parameter by applying small magnetic fields B of a few tesla along [001] and [110] but not along [111] directions [2]. The symmetry of order parameters for different field directions were determined as shown in Fig. 1. For B along [111], there is a single ordered phase of O_Z type below T_Q = 2.2 K, which is independent of B. Here we expect coexistence of three domains, where the symmetry axis Z of the quadrupole moment points along three equivalent <001> directions. The quadrupole order parameter can be conveniently represented as a two-dimensional vector with O_Z and O_X chosen to be the basis (rightmost panel of Fig. 1) [3]. For example, order parameters of the three domains for B∥[111] is given by O_Z = 3x²– r² = –O_Z/2 + √3 O_X/2 and 3y²– r² = –O_Z/2 + √3 O_X/2, corresponding to the polar angle of 0 and ±2π/√3.

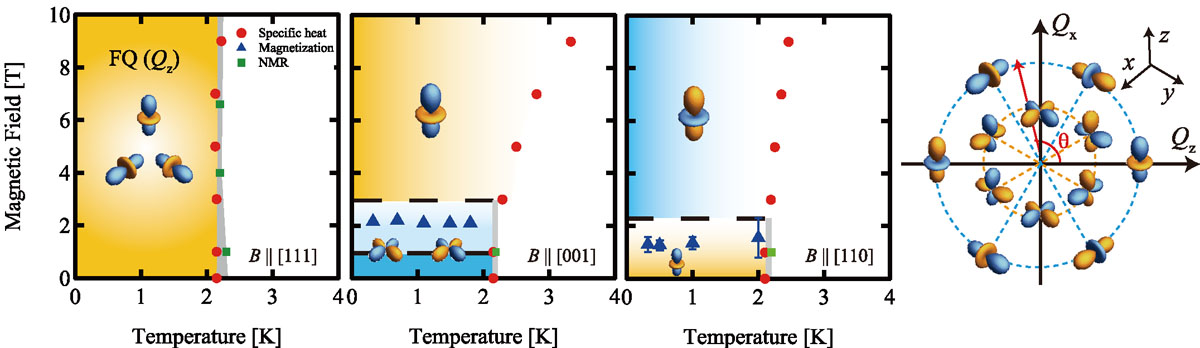
Fig. 1. The temperature vs. magnetic field phase diagram of the ferro-quadrupole order in PrTi₂Al₂₀ for B∥[111], [001], and [110]. The order parameters are indicated by graphical symbols corresponding to specific values of θ in the order parameter space shown in the rightmost panel. The phase boundaries are determined by the peak of d(C/T)/dt, C being the specific heat, splitting of the NMR lines, or kink in the Knight shift. The dashed lines for B∥[001] and [110] indicate the region of coexistence of high- and low-field phases. For B∥[001] and [110], there is no phase transition but only a crossover as a function of temperature in high fields.

For B along [001], however, discontinuous jump of the NMR frequency occurs near 2 tesla with a finite range of field where two lines coexist, indicating a first order phase transition (Fig. 2a). From the analysis of NMR spectra and magnetic susceptibility, we conclude that while the high field phase has ferro-order of O_Z with Z∥B, the order parameter of the low field phase is closer to O_X type (θ ~ ±π/2). For B along [110], the order parameter changes from O_Z with Z∥B in low fields to Z ~ –B in high fields. The field-induced transition was also confirmed by measurements of heat capacity and magnetocaloric effect [4].

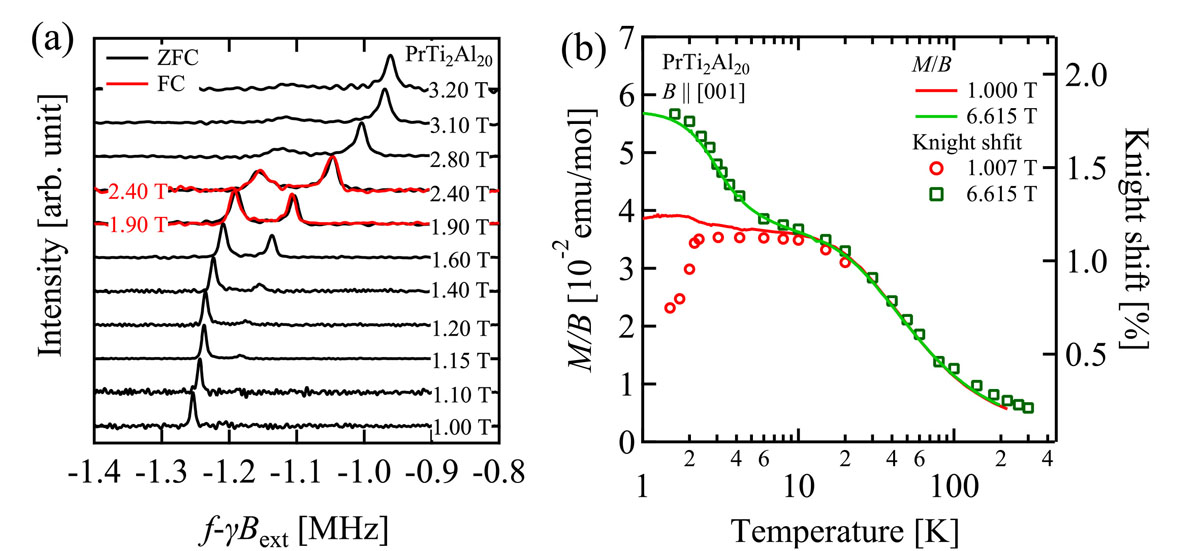
Fig. 2. (a) Magnetic-field dependence of the NMR spectrum (plotted as a function of shift from the nuclear Zeeman frequency) for B∥[001] at 1.5 K. ( b) The temperature dependences of the Knight shift at low (1T) and high (6.6T) magnetic field along [001] are compared with those of the magnetic susceptibility.

We have developed a Landau theory to identify symmetry allowed interactions between quadrupole and magnetic field, which can account for the experimentally observed switching of the order parameter [2]. Frist, the magnetic field induces mixing between Γ₃ ground doublet and excited CEF levels, leading to the van-Vleck paramagnetism. This anisotropic Zeeman interaction, which is quadratic in B, turns out to stabilize the order parameters observed in the high field phases both for B∥[001] and B∥[110], leaving only a crossover as a function of temperature. On the other hand, we found that symmetry allows interaction between quadrupoles on neighboring Pr sites, which is responsible for the ferro-quadrupole order, to depend also quadratically on B for small B. This anisotropic interaction competes against the Zeeman interaction and can stabilize the order parameter of the low field phases. Therefore, the observed switching of the order parameter can be explained if the anisotropy of the quadrupole-quadrupole interaction wins the Zeeman interaction at low fields but becomes suppressed at high fields compared with the Zeeman interaction. We have indeed succeeded in reproducing the experimental phase diagram by assuming a non-monotonic field dependence of the anisotropic quadrupole interaction.

Although the mechanism for such a non-trivial field dependence of the quadrupole interaction is not understood yet, anomalous behavior of the NMR Knight shift in the quadrupole ordered states provides an important insight. As shown in Fig. 2(b), the Knight shift at Al sites, which probes the polarization of conduction electron spin, shows the identical temperature dependence to the magnetic susceptibility at a high field (6.6T). At a low field (1T), however, they show remarkable separation below the ordering temperature, indicating that the hybridization between 4f and conduction electrons (c-f hybridization) is strongly influenced by the quadrupole order. Since the quadrupole-quadrupole interaction is mediated by the c-f hybridization, this means that the quadrupole order modifies the quadrupole-quadrupole interaction via redistribution of 4f charge density, which in turn should affect the order itself. We suspect that such a feedback mechanism may be the key to understand the field-induced discontinuous transition.

References

• [1] T. Onimaru and H. Kusunose, J. Phys. Soc. Jpn. 85, 082002 (2016).
• [2] T. Taniguchi et al., J. Phys. Soc. Jpn. 88, 084707 (2019).
• [3] K. Hattori and H. Tsunetsugu, J. Phys. Soc. Jpn. 83, 034709 (2014).
• [4] S. Kittaka et al., J. Phys. Soc. Jpn. 89, 043701 (2020).

Authors

• T. Taniguchi, K. Hattori^a, M. Yoshida, H. Takeda, S. Nakamura, T. Sakakibara, M. Tsujimoto, A. Sakai, Y. Matsumoto, S. Nakatsuji, and M. Takigawa
• ^aTokyo Metropolitan University