In a usual superconductor, electrons that have opposite momentum are bound to form a Cooper pair. Under magnetic fields, the pairs lose their stability as the field exerts forces that unbalance the electrons’ momenta. Since breaking the pairs costs an energy, however, superconductivity survives up to a certain magnetic field. Enhancing the robustness against magnetic field is technically important, e.g. for generating high magnetic fields. In the case of thin films, superconductivity is naturally robust against the in-plane magnetic field because the above-mentioned orbital breaking mechanism is suppressed due to the geometrical limitation. It would therefore be an impact if one finds approaches that make them robust against magnetic fields in other directions. We report here that for a single atomic layer superconductor narrowing terraces by steps improves the tolerance against the out-of-plane magnetic field.

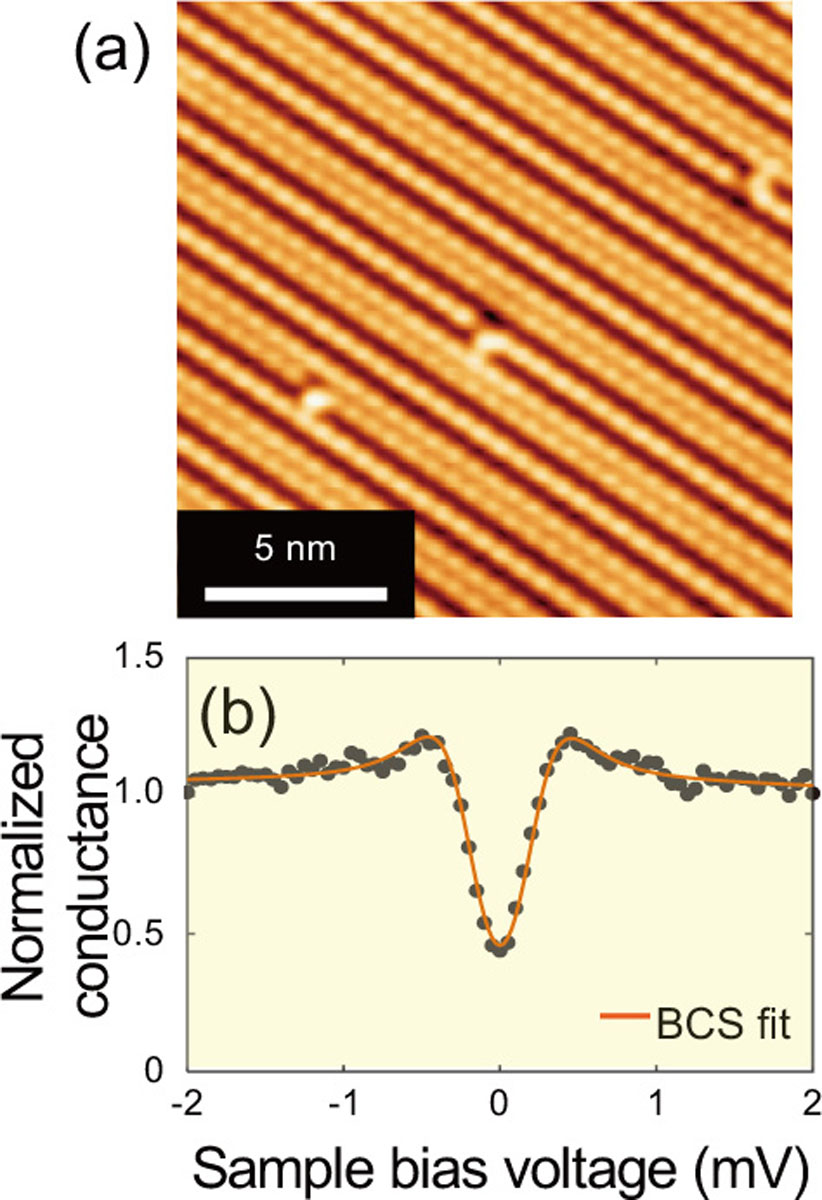
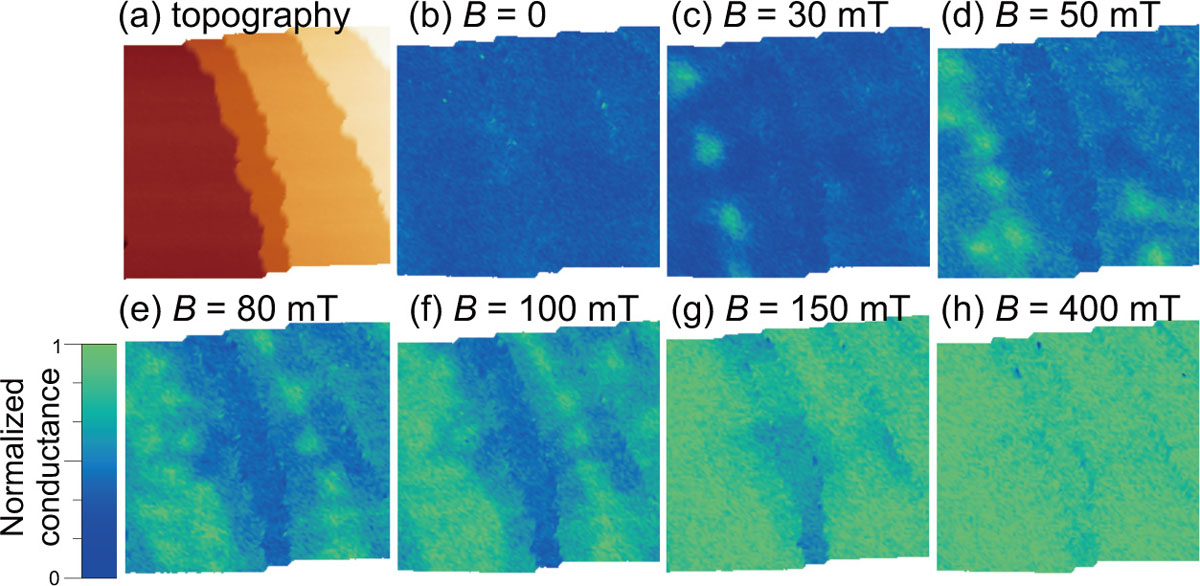
Here as a monolayer (ML) superconductor, we used a Pb-induced reconstructed structure, √3×√43 Pb/Si(111), whose nominal Pb coverage is 1.23 ML. An STM image and a tunneling spectrum taken on the structure at 0.4 K are presented in Fig. 1. From a fitting of the spectrum with the Dynes function, whose curve is drawn with a red line in Fig. 1(b), we found the gap is 0.28 meV. Figures 2(a) show an STM image taken in a wider area (1μm×1μm). The whole surface is covered with the √3×√43 phase including the area close to the step edges. In the same area as Fig. 2(a), we have taken spatial mappings of tunneling conductance at zero bias voltage (ZBC: zero bias conductance), which corresponds to the minimum conductance in the superconducting gap, under various out-of-plane magnetic fields. The amount of the magnetic field ranges from 0 to 400 mT, as shown in Figs. 2(b-h). The ZBC mapping taken under zero field (Fig. 2(b)) demonstrates almost uniform distribution of the deep gaps (low ZBC value) over the entire surface, indicting uniform superconductivity including the area of steps. The steps do not locally break the superconductivity of the ML Pb structure.

Fig. 1. (a) Atomically resolved image and (b) tunneling conductance spectrum taken on the √3×√43 Pb/Si(111) structure at 0.4 K.

When the out-of-plane magnetic fields of 30-100 mT (Figs. 2(c-f)) are applied, several round protrusions of high-ZBC (light green) area are observed. The size of the protrusion is mostly uniform and the diameter is ~100 nm. The number of the protrusions increases with the magnetic field, and the ZBC value at the center of the protrusions is almost same as the saturated ZBC measured at high magnetic fields (e.g. 400 mT of Fig. 2(h)). These features lead us to identify these protrusions as a vortex. We noticed in the mapping of 80 and 100 mT (Figs. 2(e, f)) that the vortices are formed only around the middle of wide terraces, apparently repelled from the step edges. In a narrow terrace that is observed vertically around the center of the images, no vortices are found. The apparent repelling of vortices by step edges can be explained with the presence of Josephson vortices at the step edges [1]. A Josephson vortex, formed at a Josephson junction, has an extended core along the junction with suppressed breaking of superconductivity, and therefore appeared dark (blue) along the junction, that is, along the step edges in our case. Since all the vortices including Josephson’s exhibit repulsive interaction with each other, the conventional vortices seem repelled from the step edges.

Fig. 2. (a) STM image of √3×√43 Pb/Si(111). (b-h) zero bias conductance mappings in the same field of view with (a) taken under the out-of-plane magnetic field of 0, 30 mT, 50 mT, 80 mT, 100 mT, 150 mT, and 400 mT, respectively.

In parallel with the vortex formation, the amount of ZBC behind the vortices gradually increases with the applied magnetic field. At 150 mT (Fig. 2(g)), the vortices almost lose their contrast with the background, which signals saturation of ZBC. Strikingly, in the narrow terrace, ZBC is still low, clearly demonstrating suppression of the superconductivity breaking there. In order to break the superconductivity of the narrow terrace, further increase in the magnetic field was required up to 400 mT (Fig. 2(h)), where all the area reached the saturated ZBC value. The spatially resolved ZBC evolution presented in Fig. 2 clearly demonstrates that the field that makes ZBC saturated, which corresponds to the critical magnetic field, is larger in the narrow terrace than the wide terraces.

From the ZBC evolutions we then investigated how the critical field (H_c2) depends on the terrace width w. For the quantitative analysis we first estimated H_c2 at various sites by measuring the amount of the out-of-plane magnetic field that saturates ZBC, and then dependence of the estimated H_c2 on terrace width w was investigated. Our analysis indicated a clear crossover around w = 200 nm; for w > 200 nm H_c2 is constant whereas for w < 200 nm H_c2 increases steeply with the reduction in w.

According to the Ginzburg-Landau (GL) equation, H_c2 of low dimensional superconductors whose cross-section is narrower than 2√2ξ is given by a formula of H_c2 = 4₀/πw², where w is the width (the length of short side) of the cross-section and ₀ is magnetic flux quantum. We thus expected our H_c2 measured on narrow terraces (< 200 nm) are also explained with the formula. However, H_c2 of our step-confined terraces was found markedly larger than the formula. In order to explain our results, we had to introduce a width-reduction factor w₀ in the formula as H_c2 = 4₀/π(w-w₀)2, and found good agreements with w₀ = 37 nm. The effective reduction in terrace width is probably due to the presence of Josephson vortices; their presence effectively reduces the terrace width through the modification of the boundary condition at the edges. Based on our experimental results we thus conclude that the step confinement makes the superconductor tolerant against the out-of-plane magnetic field more effectively than the geometrical confinement. It should be noted here that since the steps work as a Josephson junction, the superconductivity is not totally disconnected; coherent supercurrent flows across the steps, which is an important aspect for practical applications.

References

• [1] S. Yoshizawa et al., Phys. Rev. Lett. 113, 247004 (2014).

Authors

• F. Oguro, Y. Sato, K. Asakawa, M. Haze, and Y. Hasegawa