Heat Transport via a Two-State System
Kato Group
Heat transport in macroscopic systems has been studied for long time. Recent technological progress has enabled us to measure heat transport carried by photons or phonons via a nanoscale object, for which quantum properties of the system are revealed [1]. Based on this development, we studied heat transport in the spin-boson model, in which a two-state system is coupled to two thermal reservoirs (see Fig. 1 (a)) [2]. Even though this spin-boson model is simple, it is known that there appear various physical phenomena such as the Kondo effect [3,4].
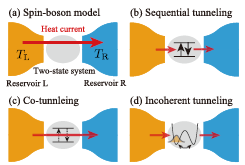
Fig. 1. (a) A schematic of the system considered in the present study. Heat transport is governed by one of three processes; (b) sequential tunneling process, (c) co-tunneling process, and (d) incoherent tunneling process.
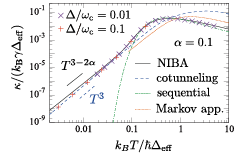
Fig. 2. Temperature dependence of the thermal conductance for the ohmic case (s = 1).
The properties of the thermal reservoirs are characterized by a spectral density function, I(ω) ∝ ωs. In Ref. [2], we studied thermal conductance for heat transport via a two-state system for arbitrary exponent s, comparing analytic approximations with numerical results based on the continuous-time quantum Monte Carlo method. By systematic comparison, we revealed that heat transport via a two-state system is described by one of three processes, i.e., (i) sequential tunneling, (ii) co-tunneling, and (iii) incoherent tunneling (see Fig. 1 (b)-(d)). We derived an asymptotically exact expression for the sufficiently low-temperature region (the co-tunneling regime). This formula predicts power-law temperature dependence at low temperatures. We also found that for the high-temperature or strong-coupling regions (the incoherent tunneling regime), the thermal conductance is well explained by the noninteracting-blip approximation (NIBA).
As an example, we show the temperature dependence of the thermal conductance for the ohmic reservoir (s = 1) and α = 0.1 (α is a dimensionless system-reservoir coupling constant) in Fig. 2. At low temperatures, the numerical result (the legends) agrees well with the asymptotically exact formula for the cotunneling process (the blue dashed line). In this regime, the thermal conductance is always proportional to T3(= T2s+1), which is consistent with the result of Ref. [4]. At moderate temperatures and high temperatures, the numerical result deviates from the cotunneling formula, and instead agrees well with the NIBA (the black solid line). We note that the thermal conductance obtained by the NIBA is proportional to T3-α at low temperatures as indicated in the figure, and deviates from the low-temperature numerical results. We also show the approximate formula for the sequential tunneling (the green dot-dashed line), and the Markov approximation for the incoherent tunneling (the orange dotted line). The former agrees with numerical data at moderate temperatures, while the latter clearly deviates from the numerical results, indicating the importance of the non-Markov properties of the system.
References
- [1] A. Ronzani et al., Nat. Phys. 14, 991 (2018).
- [2] T. Yamamoto, M. Kato, T. Kato, and K. Saito, New J. Phys. 20, 093014 (2018).
- [3] A. J. Leggett et al., Rev. Mod. Phys. 59, 1 (1987).
- [4] K. Saito and T. Kato, Phys. Rev. Lett. 111, 214301 (2013).
