Unconventional Field-Induced Spin Gap in an S = 1/2 Chiral Staggered Chain
P. A. Goddard, T. Sakakibara, and Y. Kohama
The dramatic effect of an alternating local spin environment on the properties of the spin-1/2 antiferromagnetic chain was first discovered through high-field neutron scattering and heat capacity experiments on copper-benzoate, which revealed the development of an energy gap on application of magnetic field [1]. This was perplexing until it was found that the behaviour of this system, and a handful of others, could be described by the sine-Gordon model of quantum-field theory [2,3]. Under the influence of the applied field, the gap emerges thanks to the presence of internal staggered fields and DM interactions that are a direct result of the staggered Cu(II) octahedra.
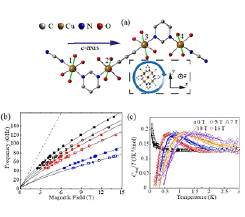
Fig. 1. (a) Chiral structure of [Cu(pym)(H2O)4]SiF6.H2O. (b) Excitations observed via electron-spin resonance at 1.9 K. (c) Temperature dependence of the magnetic contribution to heat capacity at different applied fields showing the opening of a field-induced gap. Lines are fits to a gapped model.
Here we report on the molecule-based chiral spin chain [Cu(pym)(H2O)4]SiF6·H2O (pym = pyrimidine), which at first glance could be a sine-Gordon chain, but with an added twist: a 41 screw (Fig.1(a)). Figure 1(b) shows the frequency evolution of electron-spin resonance at 1.9 K. The observed resonances (black, red and blue (open) squares) cannot be explained by paramagnetic resonances of transition metals or conventional antiferromagnetic resonance. This behavior are reminiscent of excitations observed in the sine-Gordon spin chain [pym-Cu(NO3)2(H2O)2], where the branches were identified as breather modes of the sine-Gordon model, along with six other modes more difficult to classify [4]. However, the present observation cannot be modeled by the breather gaps proposed for sine-Gordon chains. Figure 1(c) shows the magnetic contribution (Cmag) to heat capacity for a deuterated sample of [Cu(pym)(H2O)4]SiF6·H2O down to 100 mK. In zero field above 0.5 K, the nearly constant value of Cmag/T can be interpreted as the heat capacity of a uniform S = 1/2 AF Heisenberg chain in the TLL state. The heat capacity measurement also reveal the field-induced gap in [Cu(pym)(H2O)4]SiF6·H2O. Given the similarities with the nonchiral staggered chains, the expression for the temperature dependence of Cmag derived from the sine-Gordon model will provide the best possible estimate of the gap at a particular magnetic field. However fitting our data to the sine-Gordon model yields a gap of Δs = 1.98 K at 13 T, significantly smaller than the expected value of 8.24 K, calculated using g2s and J values obtained from ESR and magnetometry. More importantly, the field evolution of the gap exhibits Δs∝H, which is distinctly different from the expectation of the sine-Gordon model, where Δs∝H2/3.
To recap, electron-spin resonance, magnetometry and heat capacity measurements reveal the presence of staggered g tensors, a rich low-temperature excitation spectrum, a staggered susceptibility and a spin gap that opens on the application of magnetic field. These phenomena are reminiscent of those previously observed in non-chiral sine-Gordon systems. In the present case, however, the size of the gap and its measured linear field dependence do not fit with the sine-Gordon model as it stands. We propose that the differences arise due to additional terms in the Hamiltonian resulting from the chiral structure [5].
References
- [1] D. C. Dender et al., Phys. Rev. Lett. 79, 1750 (1997).
- [2] M. Oshikawa and I. Affleck, Phys. Rev. Lett. 79, 2883 (1997).
- [3] I. Affleck and M. Oshikawa, Phys. Rev. B 60, 1038 (1999).
- [4] S. A. Zvyagin et al., Phys. Rev. Lett. 93, 027201 (2004).
- [5] J. Liu et al., Phys. Rev. Lett.122, 057207 (2019).
