Electric Dipole Spin Resonance in the Interacting Quantum Spin Dimer System KCuCl3
S. Kimura, M. Matsumoto, and M. Akaki
The observation of optical transition from spin singlet to triplet states by means of high frequency electron spin resonance (ESR) measurements is known as an advantageous tool to investigate the energy spectrum of quantum spin gap systems, such as a Haldane system or a spin ladder, in high accuracy. The transition has been reported for many spin gapped system, for instance Ni(C2H8N2)2NO2ClO4 (NENP), CuGeO3 and SrCu2(BO3)2. However, the singlet-triplet transition is, in principle, forbidden in magnetic dipole transition, and therefore the origin of its finite transition probability is not so clear at the moment.
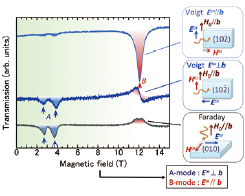
Fig. 1. ESR signals of the singlet-triplet transitions in KCuCl3, observed in the Faraday and Voigt configurations. In the measurements in the Voigt configuration, linearly polarized electromagnetic wave is illuminated to the sample. The ESR signals A and B come from the higher and lower triplet excitation modes, respectively. The experimental result shows that both signals are electrically driven, and directions of the oscillating electric fields, which couples to A and B, are orthogonal each other.
Here we report on our recent high frequency ESR study on the S = 1/2 interacting dimer system KCuCl3. By measuring polarization dependence of the ESR signal, we have clarified that the singlet-triplet transition in this compound is due to the electric dipole transition [1]. In KCuCl3, spin dimers composed of two Cu2+ spins form a three dimensional network in the monoclinic crystal. Reflecting this dimer structure, the ground state of this compound is the spin singlet state, and does not order down to the lowest temperature. From the previous measurements, two sets of the singlet-triplet transitions were observed [2]. The two sets of the singlet-triplet transitions are due to two kinds of the crystallographically different dimers in the unit cell of KCuCl3, which gives rise to superposition of two kinds of the triplet excitation modes in the momentum space. To determine the selection rules of the singlet-triplet transition, we have performed the high frequency ESR measurements by illuminating linearly polarized electromagnetic wave to the sample.
Figure 1 shows the ESR signals from the singlet-triplet transition in KCuCl3 in external magnetic fields parallel to the b axis. Our experiment showed that both the lower and higher energy triplet modes A and B couple with oscillating electric fields of the electromagnetic wave. Furthermore, the directions of the oscillating electric fields, which couple to the A and B modes, are orthogonal each other. These behaviors are explained by the spin dependent electric polarization. Recent studies for magntoelectric multiferroic materials revealed that the vector spin chilarity Si × Sj, which is an outer product of neighboring spin, induces an electric polarization P, as P = C̃ (Si × Sj), where C̃ is a second rank tensor. Coupling between this P and the oscillating electric fields Ee-iωt can be regarded as a dynamical Dzyaloshinsky-Moriya (DM) interaction, oscillating with an angular frequency ω. Because DM interaction has finite matrix elements between spin singlet and triplet states, the electric dipole transition between these states can occur. By taking into account the two-fold helical axis between the two dimers, the observed characteristic selection rule of the singlet-triplet transition is also explained. The electric polarization, generated by Si × Sj, can appear regardless of the local structural symmetry between the two spin sites. Therefore, electric dipole spin resonance by the spin-dependent electric polarization is universal for spin gapped systems. It is possible that the singlet-triplet transitions that were previously observed in various spin gapped materials are induced by this polarization mechanism.
References
- [1] S. Kimura, M. Matsumoto, M. Akaki, M. Hagiwara, K. Kindo, and H. Tanaka, Phys. Rev. B 97, 140406 (2018).
- [2] H. Tanaka, K. Takatsu, W. Shiramura, T. Kambe, H. Nojiri, T. Yamada, S. Okubo, H. Ohta, and M. Motokawa, Physica B 246-247, 545 (1998).
- [3] H. Katsura, N. Nagaosa, and A. V. Balatsky, Phys. Rev. Lett. 95, 057205 (2005).
- [4] T. A. Kaplan and S. D. Mahanti, Phys. Rev. B 83, 174432 (2011).
