We have investigated thickness dependence of the electronic properties of two layered semimetals, graphite and WTe₂, under magnetic fields. Their monolayer limits are known as a 2D Dirac fermion system (graphene) and a 2D quantum spin Hall insulator, respectively. Therefore, it is significant to see how their electronic properties changes associated with thinning them.

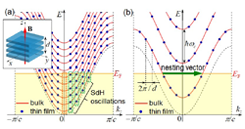
Fig. 1. Concept of the quantum size effect under magnetic fields. The Landau subbands in the bulk (red curves) are quantized into discrete levels (blue circles) due to the size effect in thin films. (a) In the low field region, several SdH oscillations with different frequencies appear in thin films, instead of the oscillation of the extremal orbit in the bulk. (b) At the high-field quantum limit, the field-induced density wave transition due to the 2kF instability of the lowest subband is suppressed by the discretization of the subband.

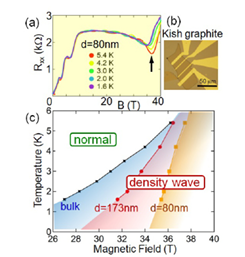
Fig. 2. Quantum size effect on the field-induced electronic phase transition in graphite. (a) Transverse magnetoresistance of a graphite thin film with the thickness of 80 nm. The arrow indicates the field-induced transition. (b) Microscope image of a Kish graphite thin film device. (c) Phase diagram of the field-induced transition in graphite thin films.

Generally, under the normal magnetic field, the band structure of the layered conductor is quantized to a set of Landau subbands with interlayer dispersion. Here, as the sample thickness approaches the de Broglie wavelength, the interlayer electron wave number is quantized, so that the bulk Landau subbands separates to discrete levels as shown in Fig. 1. This causes various size effects on electronic properties.

Bulk graphite shows a unique field-induced electronic phase transition above 30 T. Although the density wave formation due to the 2k_F instability of the Landau subband was proposed as a possible mechanism of the transition, it has never been confirmed yet. In order to identify the high field phase, we performed transport measurements of thin-film graphite samples under the magnetic field up to 40 T, which was generated by a home-made miniature pulse magnet system. The thin-film flake was prepared on a silicon substrate by the mechanical exfoliation technique, and the device structure was fabricated using the electron beam lithography (Fig. 2(b)). As seen in Fig. 2(a), the magnetoresistance shows a saturation around 10 T, above which there exist only a few occupied Landau subbands (quasi-quantum limit). The field-induced phase transition appears above 30 T as indicated by an arrow. On the phase diagram, the phase boundaries in thin films shift to higher fields, accompanied by a reduction in temperature dependence. These results are consistently explained by the density wave model with the quantum size effect, because the 2k_F instability of the Landau subband is weakened by the discretization of the subband in thin films (Fig. 1(b)). The present finding strongly suggests the density wave state standing along the interlayer direction [1].

The bulk crystal of a layered transition metal dichalcogenide compound, 1T'-WTe2, is known as a 3D type-II Weyl semimetal. In order to see the change of topological states, we carried out the magnetotransport measurement of WTe₂ thin films with reducing their thickness. Since WTe₂ is degraded in the atmosphere, the mechanical exfoliation process was performed in the grove box. The clear Shubnikov-de Haas (SdH) oscillations are observed on positive magnetoresistance. The FFT spectrum of the SdH oscillations has mainly four peaks, which correspond to the extremal orbits surrounding four Fermi surfaces of the bulk. Their peak frequencies start to decrease with a film thickness of about 50 nm or less. Moreover, as the film thickness decreases, many weak subpeaks appear on the low frequency side of each main peak below about 30 nm. According to the picture of the quantum size effect (Fig. 1(a)), the observed subsidiary SdH oscillations with different frequencies originate from the 2D subbands, to which the bulk band with a Fermi surface is quantized.

References

• [1] T. Taen, K. Uchida, and T. Osada, Phys. Rev. B 97, 115122 (2018).

Authors

• T. Osada, T. Taen, H. Adachi, T. Uchida, and K. Uchida