Spin degeneracy of conducting electrons in materials can be lifted by spin-orbit interaction (SOI). Here, the symmetry of a surface or interface plays an important role in determining the spin splitting and texture of a 2D band. [1] In the framework of the Rashba model for a two-dimensional (2D) electron gas, a free-electron-like band dispersing from the Γ point is shifted oppositely in the wave number direction by SOI, depending on the spin direction that is perpendicular to both the surface normal and momentum of the electron. Another type of the spin-split band in the 2D system is called the Zeeman type, where the spin direction is perpendicular to the 2D plane without spin degeneracy at the symmetry point in the wave-number space. In the case of the spin-split bands of the surface 2D electron system with a three-fold lattice symmetry, either the Zeeman- or Rashba-type spin splitting has been considered to appear around a K point exclusively depending on the crystal symmetry. [1]

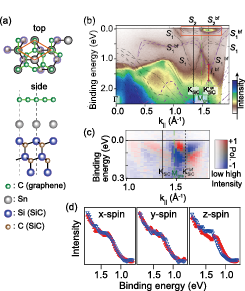
Fig. 1 (a) Atomic structure model of a Sn TLAL intercalated into the graphene/SiC(0001) interface. (b) ARPES intensity image of the Sn TLAL along ΓKSiC with overlaying the calculated band structure. The color scale represents the photoelectron intensity, and gray (purple) dashed curves the original (back-folded) bands. Two surface bands, S₁ and S₂, and their back-folded bands, S₁^bf and S₂^bf, are marked. (c) SARPES intensity images taken with the region including S₂ and S₂^bf bands near EF surrounded by a thin rectangle in (b). The y-spin polarization component is detected. The two-dimensional color scale represents both the photoelectron intensity and the spin polarization. (d) The x, y, and z components of the spin-resolved spectra in the region marked as l₁ at K’_SiC^bf of S₁^bf band in (b).

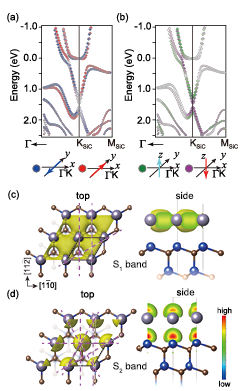
Fig. 2. (a,b) Spin polarization in the y (a) and z (b) directions for the bands around KSiC, where the opposite spin directions are indicated by blue-red and green-purple colors, respectively. The diameter of the circles is proportional to the total contribution of Sn 5s and 5p. (c,d) Charge density distributions for the Zeeman-like spin-split band of S1 (c) and the Rashba-like spin-split band of S₂ (d) at the KSiC point. Left (right) panels represent top (side) views. In the left panels, the solid parallelograms show the unit cell of Sn/SiC(0001)-(1 × 1). The dashed lines indicate the mirror planes of the charge density distribution.

We have found a novel spin-dependent band structure of a Sn triangular-lattice atomic layer (TLAL) at the K point. The sample is formed by intercalation into the interface between graphene and the SiC(0001) substrate as a schematic model shown in Fig. 1(a). [2] At the K point of the Sn TLAL with the symmetry of C₃ according to the lattice symmetry p3m1, the Zeeman-type spin splitting is reasonably explained by the symmetry while the Rashba-type band crossing is not expected. Using our spin- and angle-resolved photoelectron spectroscopy (SARPES) with three-dimensional spin detection [4] and He Iα (hν ~ 21.22 eV) radiation, both the Zeeman-type and Rashba-type spin splits are confirmed at the K (K’) point as shown in Fig. 1(b-d). [4] The surface band S₂ near E_F exhibits a Rashba type inconsistently with the lattice symmetry, while the surface band S₁ around 1.5 eV below EF is the Zeeman type as expected. It should be noted that the photoelectron intensity for the back-folded band around the K’ point due to the graphene-lattice scattering is stronger than that of the original one around the K point in the present experiment conditions.

We have investigated the origin of the two types in the Sn TLAL by evaluating the spin-resolved band structure and charge distribution for the spin-split bands using density functional theory calculations. The directions of the spin polarization are well reproduced by the calculation as in Fig. 2(a,b). The calculated charge distribution of the Rashba-type (Zeeman-type) band at the K point, shown in Fig. 2(c,d), corresponds to a C_3v (C₃) symmetry at the K point. Theoretically, the C_3v symmetry allows the Rashba-type band crossing regardless of the existence of the time reversal symmetry. [1] The symmetry of the charge density distribution, which is still a consequence of the crystal field potential for the electrons, is a key to understand the nature of the spin splitting due to SOI.

References

• [1] T. Oguchi and T. Shishidou, J. Phys. Condens. Matter 21,092001 (2009).
• [2] S. Hayashi et al., Appl. Phys. Express 11, 015202 (2018).
• [3] K. Yaji et al., Phys. Rev. Lett. 122, 126403 (2019).
• [4] K. Yaji et al., Rev. Sci. Instrum. 87, 053111 (2016).

Authors

• K. Yaji, A. Visikovskiy^a, T. Iimori, K. Kuroda, S. Hayashia, T. Kajiwara^a, S. Tanaka^a, S. Shin, and F. Komori
• ^aKyushu University