Recent progress in ultrafast laser technology has realized to produce strong optical fields in the mid-infrared to terahertz spectral regions. Emergence of such intense long-wavelength light sources triggers ultrafast strong-field physics for condensed matters. When crystalline materials are irradiated by intense mid-infrared pulses, for example, extreme ballistic oscillation of electrons in a conduction band with terahertz to petahertz frequencies occurs, and high-order harmonics are often produced beyond a typical bandgap of solids. So far, most of the experiments employ one-dimensional study along a specific direction. However, we show that a one-dimensional model is not suitable to investigate polarization property of HHG in solids.

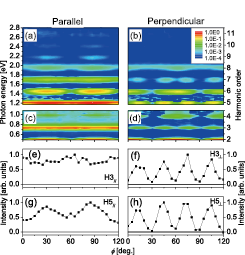
Fig. 1. Polarization resolved measurement of the crystallographic orientation dependence of high harmonics generated in GaSe with a high field amplitude of 10 MV/cm. Parallel (a, visible; c, infrared) and perpendicular (b, visible; d, infrared) polarization components of the high harmonics. Curve plots of the parallel third (e), perpendicular third (f), parallel fifth (g), and perpendicular fifth (h) harmonics.

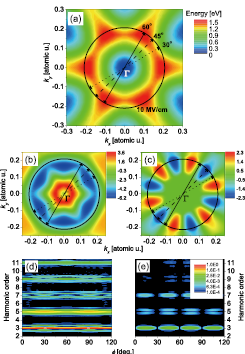
Fig. 2. Calculated results by the two-dimensional single-band model. (a) Lowest conduction band of GaSe and its band curvatures. (b) the band curvature component responsible for parallel odd harmonic generation. (c) the other band curvature component responsible for perpendicular odd harmonic generation. Three electron trajectories at φ = 60° (solid black arrows), 45°(dash), and 30°(dot) are illustrated. The maximum amplitude of electron trajectories with an electric field of 10 MV/cm is shown by the black circle. Orientation dependence of the (d) parallel and (e) perpendicular harmonics obtained by the two-dimensional single-band model with the 10-MV/cm electric field.

In this study, we investigate polarization properties of high harmonics produced in a 30-µm-thick gallium selenide (GaSe, ε-type, [001] z-cut, hexagonal structure, non-coat). The crystal is exposed to linearly polarized femtosecond mid-infrared pulses with a field amplitudes of ~10 MV/cm that are produced from a dual-wavelength optical parametric amplifier (wavelength: 5 µm, maximum pulse energy: 15 µJ, pulse duration: 200 fs, repetition rate: 1 kHz) [1]. The crystallographic orientation dependence of high harmonic spectra is measured after a set of wire-grid polarizers in the either parallel (Fig. 1(a), (c), (e), and (g)) or perpendicular (Fig. 1(b), (d), (f), and (h)) to the mid-infrared field. The observed high harmonics are extended up to the 11th order (2.70 eV, 460 nm) beyond the bandgap (1.98 eV, 625 nm). All even harmonics for both polarizations show modulations with 60° periodicities, which is consistent with the hexagonal structure of a GaSe crystal. In contrast to the even harmonics, the parallel and odd harmonics show 60° modulation on top of a constant offset as in Figs. 1 (e) and (g) for the third and fifth harmonics, respectively. More surprisingly, the perpendicular odd harmonics appear with 30° periodicity as can be seen in Figs. 1(f) and (h). This 30° periodicity cannot be intuitively understood from the hexagonal structure of the crystal.

To explain these results, a two-dimensional single-band model described by the Bloch theorem is used [2]. This model assumes that (i) the intraband current dominates odd harmonics and (ii) the electron wavepacket is launched around the Г point. Detailed explanation of the model and a verification of these assumptions can be found in Ref. [3]. We found that the band curvature (Figs. 2 (b) and (c)) of the lowest conduction band (Fig. 2(a)) along the electron trajectory is responsible for the source of odd-order harmonics. Based on the two-dimensional single-band model, the parallel and perpendicular odd harmonics are calculated to show 60° and 30° periodicities as can be seen in Figs. 2(d) and (e), respectively. These results well reproduce the experimental observations of the orientation dependences and the polarization property for all odd harmonics.

In summary, we have investigated a polarization property of high harmonics from a bulk GaSe crystal using femtosecond MIR pulses and their dependence on crystallographic orientation. With the 10 MV/cm electric field, the perpendicular odd harmonic emerges with a periodic modulation of 30°, which cannot be explained by the perturbative nonlinear optics. The underpinned physics of the perpendicular component of the odd harmonics is attributed to anisotropic momentum dependence of the band curvature along the electron trajectory, which is equivalent to the inverse effective mass. Our demonstration establishes a direct link between the band structure and HHG in a crystalline solid. Multi-dimensional analysis combined with time-resolved measurement allows to investigate electron dynamics and field-dressed structure of energy bands in future.

References

• [1] K. Kaneshima, N. Ishii, K. Takeuchi, and J. Itatani, Opt. Express 24, 8660 (2016).
• [2] S. Ghimire, A. D. DiChiara, E. Sistrunk, P. Agostini, L. F. DiMauro, and D. A. Reis, Nature Phys. 7, 138 (2011).
• [3] K. Kaneshima, Y. Shinohara, K. Takeuchi, N. Ishii, K. Imasaka, T. Kaji, S. Ashihara, K. L. Ishikawa, and J. Itatani, Phys. Rev. Lett. 120, 243903 (2018).

Authors

• K. Kaneshima, Y. Shinohara^a, K. Takeuchi, N. Ishii, K. Imasaka^b, T. Kaji^b, S. Ashihara^b, K. L. Ishikawa^{a, c}, and J. Itatani
• ^aPhoton Science Center, School of Engineering, The University of Tokyo
• ^bInstitute of Industrial Science, The University of Tokyo
• ^cDepartment of Nuclear Engineering and Management, School of Engineering, The University of Tokyo