From Gapless Kitaev Spin Liquid to Classical String Gas through Tensor Networks
Kawashima Group
Quantum spin liquids (QSLs) represent a state of quantum matter which is not characterized by any local order parameters even at zero temperature. These novel states are expected to exhibit long-range entanglement leading to the topological order and fractionalized excitations. For example, the Haldane phase, which is known as a symmetry-protected topological phase, is a fascinating phase one can find in the S=1 quantum spin chain. The novel character that discriminates the Haldane phase from trivial gapped states was most clearly revealed by the discovery of Affleck-Kennedy-Lieb-Tasaki (AKLT) model and its exact ground state or the AKLT state. Its compact representation in the form of a matrix-product state provided a new insight into the Haldane phase. As a two-dimensional system with spin-liquid state, the Kitaev model on honeycomb lattice (KHM) is now a subject of active research, due to recent successful realizations of Kitaev materials. The model is exactly solvable and exhibits gapless and gapped Kitaev spin liquid (KSL) ground states with fractionalized excitations.
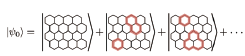
Fig. 1. Schematic representation of the "loop-gas" state. It is a sum of all loop-gas configurations. Each configuration corresponds to a product of Pauli operators. The loop-gas configuration determines which Pauli operator is aligned on a given lattice.
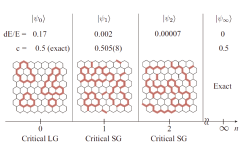
Fig. 2. The series of ansatze converging to the exact KHM ground-state. The zero-th one is the loop-gas state. The energy of the second order approximation already attains 4-digit accuracy, which has never been achieved by other numerical variational methods.
In the present work, we propose a "loop-gas" state, i.e., an exactly-solvable quantum state that has a compact and exact tensor-network representation, and a series of ansatze that starts from the loop-gas state and converges rapidly to the KHM ground-state. The loop gas state is defined by the loop-gas projector applied to a product state in which all spins are aligned in the (111) direction. The loop-gas projector is defined as tensor-network operator with bond-dimension 2, which is represented by a sum of all loop configurations each corresponding to a product of Pauli operators on all lattice points. (Fig. 1) We find that the norm of the loop gas state is exactly the same as the classical loop gas model at the critical fugacity on honeycomb lattice. The classical loop gas model appears in the low-temperature expansion of the Ising model, and therefore shares the same critical properties as the latter. These observations establishes that the correlation function of the loop-gas state is exactly the same as the correlation function of the critical Ising model. Furthermore, by defining the dimer-gas operator in an analogous way to the loop-gas operator, and applying it to the loop-gas state, we can improve the loop-gas state as an approximate to the KHM ground-state. (Fig. 2) For example, the second order approximation, which is obtained by applying the dimer-gas operator twice, achieves more than 4-digits accuracy in the energy. This is better than any other previous variational wave function. Also, note that there are only two adjustable parameters in the ansatz.
From these results, we conclude that the series of ansatze starting from the loop-gas state correctly reflects the essential properties of the family of KSLs, which is known to belong to the Ising universality class. Since the present description of KSLs does not rely on the mapping to fermions, it provides us with an alternative view point to discuss KSLs.
References
- [1] H.-Y. Lee, R. Kaneko, T. Okubo and N. Kawashima: arXiv:1901.05786.
