As materials are cooled down towards the absolute zero temperature, generally they become a solid with a long-range order in location of atoms. Likewise, magnetic materials develop a magnetic long-range order at sufficiently low temperatures. However, we may expect a “quantum spin liquid” as a ground state of a magnetic material, if strong quantum fluctuations destroy the magnetic order even at zero temperature. Theoretical studies have revealed that quantum spin liquids exhibit various exotic phenomena such as fractionalization. Its realization has been one of the central topics in quantum magnetism and condensed matter physics. After intensive studies over several decades, several materials have been found to be strong candidates of quantum spin liquids. However, such candidate materials are still limited, and it is desirable to find new class of quantum spin liquid materials.

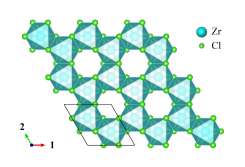
Fig. 1. Crystal structure of α-ZrCl₃. Zr³⁺ ions form a honeycomb lattice.

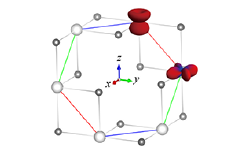
Fig. 2. Hexagonal plaquette of α-ZrCl₃. Hoppings between anisotropic d-orbitals are strongly orbital-dependent, and also depend on the bond directions indicated by colors (red, blue, and green).

Quantum magnets often possess the (approximate) spin rotation symmetry. Mathematically it corresponds to the group of “rotations” of two-component complex vectors, SU(2). Here the two components of the vector correspond to the amplitudes of the spin pointing up and down. It is then natural to consider an extended symmetry of “rotations” of N-component complex vectors, SU(N). For a larger N, the symmetry is larger, and the quantum fluctuations would be stronger. In fact, there have been numerous theoretical studies of SU(N) “spin” systems, many of which are found to be quantum spin liquids. Experimentally, the SU(N) symmetry has been realized using nuclear spin degrees of freedom in cold atoms. However, it is still difficult to observe the SU(N) quantum spin liquid behavior in cold atoms, it is desirable to realize it in a magnetic material.

In principle, the SU(N) symmetry can appear if there are degenerate orbitals which can be occupied by electrons. For example, there are two degenerate orbitals in each atom, an electron can take 2 orbital states and 2 spin states, namely 4 states in each atom. If the system is symmetric with respect to the “rotation” of these 4 states, it is SU(4) symmetric. However, since the orbital and spin are completely different degrees of freedom, there is no particular reason to expect the SU(4) symmetry. In fact, it has been known that the standard model of electrons in the presence of two degenerate orbitals, Kugel-Khomskii model, has the SU(4) symmetry only at a special point, which would require a fine-tuning. Indeed, no material has been known to possess the SU(4) symmetry, even approximately.

In this work [1], we demonstrate theoretically that the SU(4) symmetry emerges in α-ZrCl₃ (Fig.1). In the limit of strong spin-orbit coupling, the effective model of electrons in this material has strongly orbital-dependent hoppings (Fig. 2). As a result, the model looks far from SU(4) symmetric. However, the electron hopping between neighboring Zr ions can be identified with an SU(4) gauge field on the lattice. We find that, with an appropriate SU(4) gauge transformation on the lattice, the model is mapped to a manifestly SU(4)-symmetric one (Kugel-Khomskii model at the SU(4) point). This means that α-ZrCl₃ has an emergent SU(4) symmetry, despite the strong spin-orbit coupling which seems to destroy even the spin SU(2) symmetry. In the strong electron repulsion limit, the effective model is reduced to the SU(4) “antiferromagnetic Heisenberg” model, which has a gapless spin liquid ground state according to a preceding theoretical study. Therefore, we expect that α-ZrCl₃ realizes an SU(4)-symmetric quantum spin liquid. In fact, the SU(4) symmetry means that the spin and orbital degrees of freedom are intertwined and fluctuating together. In this sense, the ground state should be better called a quantum spin-orbital liquid.

References

• [1] M. Yamada, M. Oshikawa, and G. Jackeli, Phys. Rev. Lett. 121, 097201 (2018).

Authors

• M. Yamada, M. Oshikawa, and G. Jackeli^a
• ^aUniversity of Stuttgart and Max-Planck Institute for Solid State Research