The concept of spin-charge separation plays a central role in describing low-energy physics near Fermi points in a one-dimensional (1D) interacting electron gas, a typical example of the spin-1/2 Luttinger liquid (LL). This concept may be confirmed in real materials by various experiments, including the recent high-resolution angular resolved photoemission spectroscopy in which the one-electron spectral function A(p,ω) can be directly measured in the wide range of momentum p and energy ω.

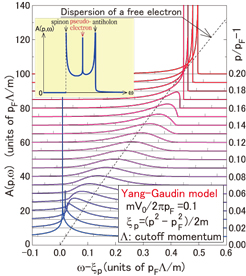
Fig. 1. Structural change of the pseudoelectron peak in the one-electron spectral function A(p,ω) for the Luttinger liquid (Yang-Gaudin model). Inset: The entire structure of the spectral function near the Fermi point.

If p is not restricted to the region near the Fermi momentum p_F, the linear spectrum approximation, usually adopted in the LL theory, is not sufficient in appropriately obtaining A(p,ω). In fact, the effect of the nonlinear spectrum on A(p,ω) has been intensively studied in recent years. According to those studies on integrable systems, A(p,ω) has singularities for arbitrary p in proportion to |ω-ε_ν(p)|^-μ_ν^(p) with ν=s and c, where ε_s(p) and ε_c(p) are energies of spin and charge collective excitations, respectively. In the usual LL theory, the exponent μ_ν(p) is independent of p, but the nonlinearity in the electron dispersion makes it depend on p. Since the edge of support of A(p,ω) is located at ω=ε_s(p), μ_s(p) determines the power of the threshold singularity in A(p,ω) and its actual value has been given from the finite-size spectrum obtained by the Bethe-ansatz method. For nonintegrable systems, this threshold singularity remains intact, but the singularity at ω=ε_c(p) is smeared into a broad peak.

In those preceding works, only the singularities at ω=ε_s(p) and ω=ε_c(p) are discussed on the belief that the electron nature will not sustain in the spin-charge separated system. For p far away from p_F, however, the effect of interactions becomes so weak that we would naively expect that the nature of an injected electron to measure A(p,ω) manifests itself as a main peak in A(p,ω). Then a natural question arises: Does an electron-like excitation mode actually exist in the 1D interacting electron gas for p much larger than p_F? If yes, a related and more intriguing question is: How does the electron-like mode reconcile with the physics of spin-charge separation for p near p_F?

In pursuit of answers to those questions, we have carefully studied the 1D one-electron Green's function G(p,t) in momentum space and time and found that for p~p_F, its long-time asymptotic form is composed of three independent modes of power-law decay [1]. Two of them correspond to well-known spinon and (anti)holon excitations, but the rest describes the mode of an electron-like particle (pseudoelectron) which may be regarded as an electron dressed with a “cloud” of low-lying spin and charge collective excitations. This pseudoelectron does not appear as a main structure in A(p,ω) for p~p_F and never leads to a finite jump in the momentum distribution function n(p). As p goes away from p_F, the pseudoelectron structure gets broader, but with the further increase of p, it becomes less broad and eventually for p>>p_F, it evolves as a main and divergent peak in A(p,ω) by swallowing the antiholon mode. Concomitantly, its dispersion relation approaches the one of a free electron, allowing us to regard the pseudoelectron as a free electron, but actually it is not quite, nor the Landau's quasiparticle, basically because this excitation is accompanied by power-law decay. Those results clarify the generic feature of A(p,ω)in a 1D metal and answer the aforementioned two questions.

As an illustration of the overall behavior of A(p>p_F,ω) with the change of p and ω, we adopt the Yang-Gaudin model in the weak-coupling region in order to explicitly compute A(p,ω). In Fig. 1, the obtained result is displayed with increasing p from p_F to show its complete structural evolution in the 1D weakly-interacting electron gas with the quadratic dispersion ξ_p (=p²/2m-p_F²/2m). Since we focus on the region of ω in the very vicinity of ξ_p, only the pseudoelectron mode appears as a singular structure in A(p,ω) in Fig. 1.

The pseudoelectron introduced here very much resembles a quasiparticle in higher-dimensional Fermi-liquid systems, although it is not quite the same, reflecting the specialty of 1D physics. We hope that this concept of a pesudoelectron will be confirmed in the future through experiment and/or large-scale numerical calculation with deliberately-chosen parameters so as to avoid its overdamping regime.

References

• [1] H. Maebashi and Y. Takada, Phys. Rev. B 89, 201109 (R) (2014).

Authors

• H. Maebashi and Y. Takada