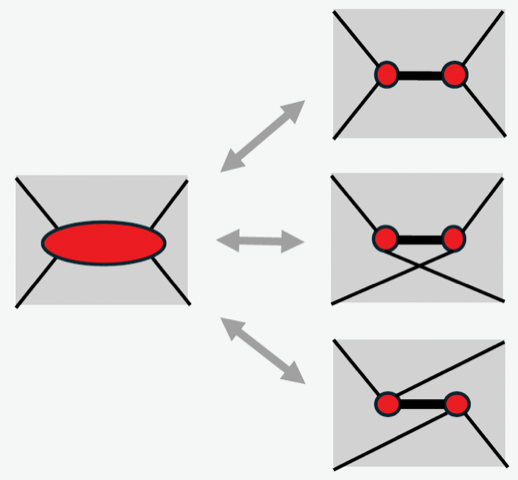
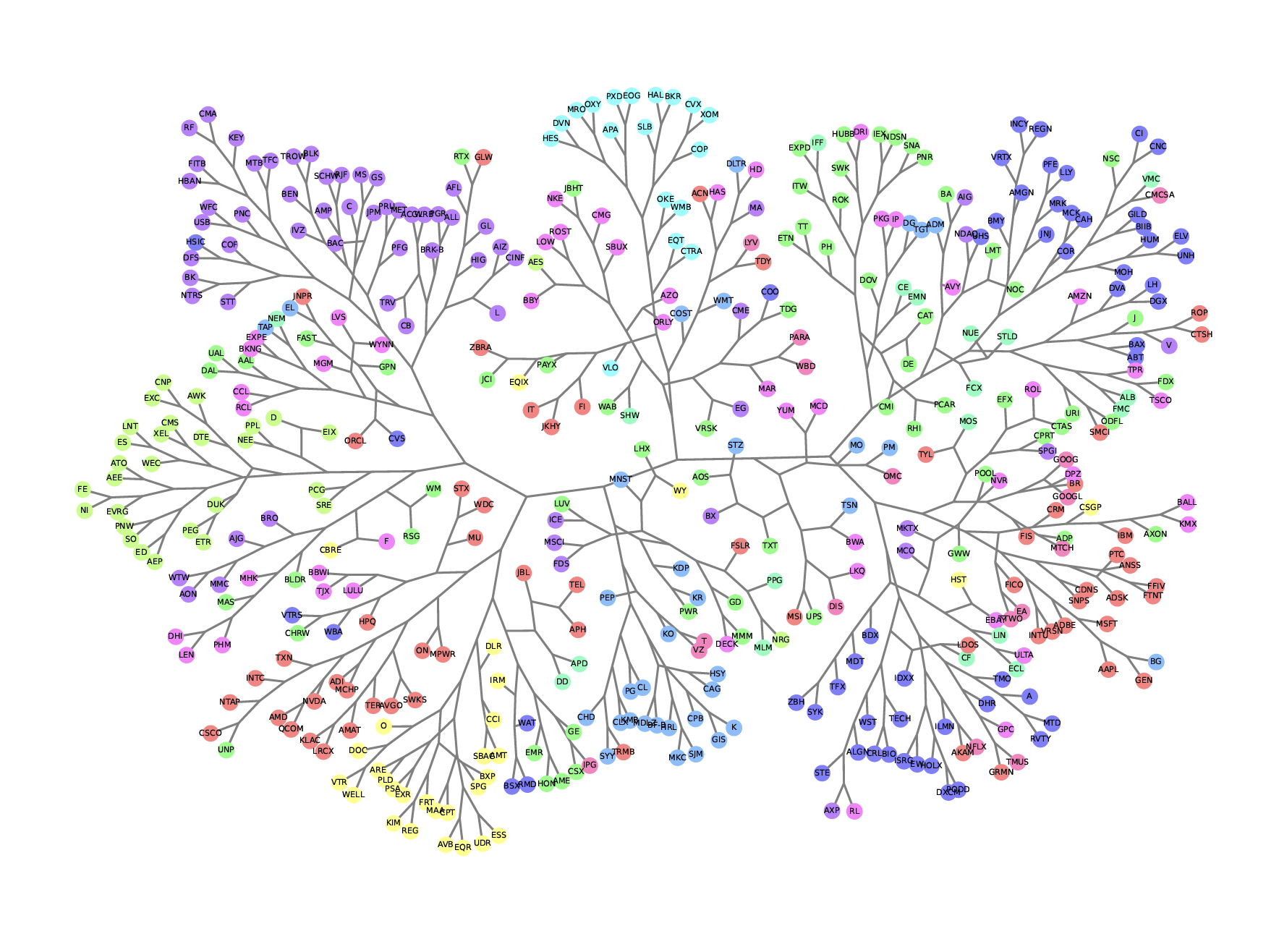
Recently, the popularity of artificial intelligence, machine learning, and quantum computing has drawn a lot of attention to computers in society. Our research group is conducting research to clarify the mathematical core of computational statistical mechanics and developing new methods. As applications of these methods, we are trying to solve various problems in statistical mechanics and strongly correlated electron systems to compare with experimental research. The quantum Monte Carlo method and tensor network method used there also have connections with data science through Boltzmann machines and data compression. In particular, the tensor network method has been developing rapidly in recent years, and we are exploring the possibility of applying this method to general data analysis. For example, we have succeeded in constructing a generative model using a tree-type tensor network that acquires a probability distribution function that realizes a given multivariate sample set. This generative model is characterized by its automatic optimization of the network structure, and we hope that it will open up new possibilities for machine learning.

• Publications
• Research Highlights