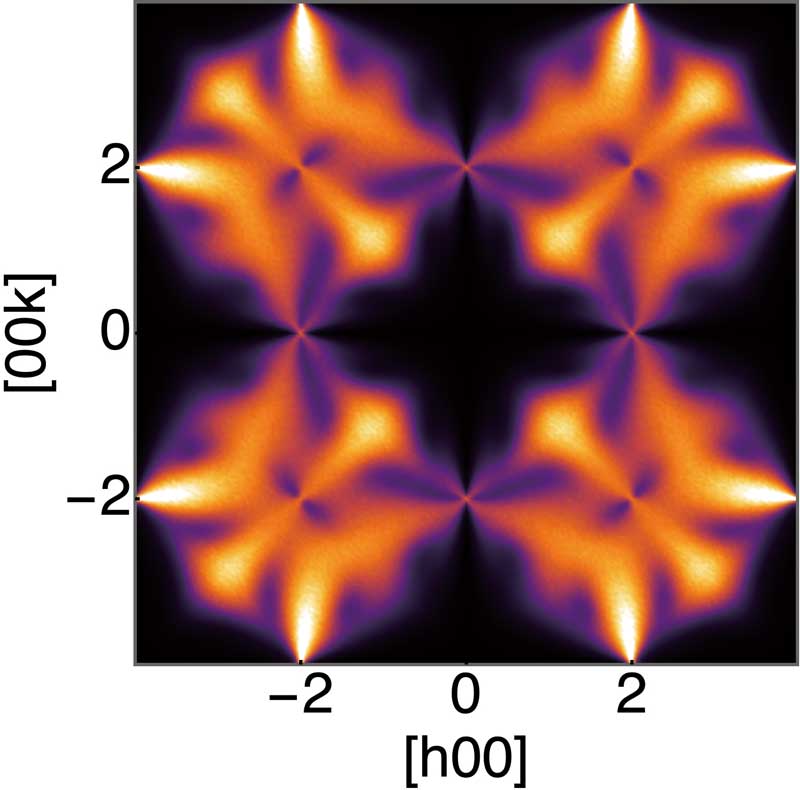
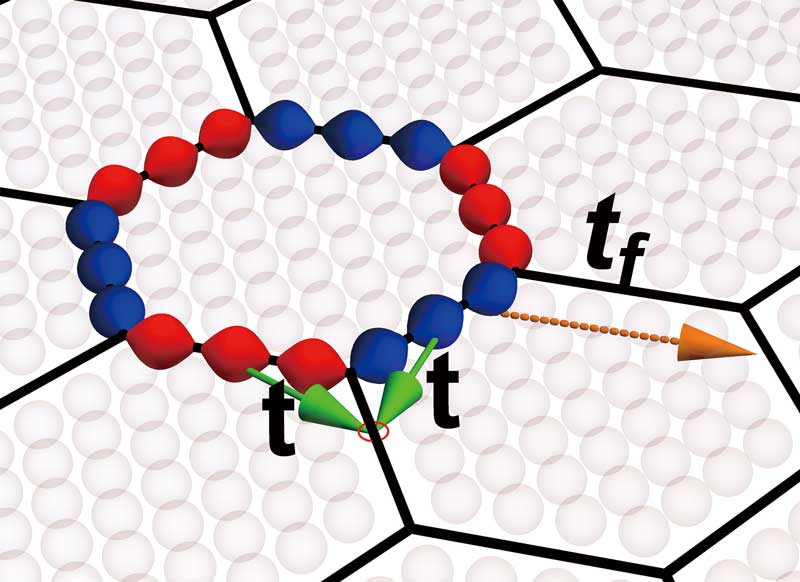
We pursue universal concepts in physics, especially in quantum many-body systems. As an example, based on anomaly in quantum field theory, we introduced a new classification of gapless quantum critical phases in the presence of symmetries. This opened up a new direction in classification of quantum phases. On the other hand, taking advantage of novel theoretical concepts, we also aim to give a unified picture on experimental data and to make testable predictions for experiments. For example, recently we introduced a “network model” of quantum wires in order to describe electronic states in the charge-density-wave material 1T-TaS2 and demonstrated a realization of flat bands. Unlike most of the known constructions of flat bands, in our novel mechanism, the flatness is protected by symmetries and is robust. Furthermore, we investigate possible realizations of higher-rank gauge theories and fracton topological phases in frustrated magnets and their experimental consequences. Much of our research is carried out in international collaborations.

• Publications
• Research Highlights