Combining different materials in artificial nanostructures is a most important approach to create improved or even completely new electronic functionalities for technological applications. A very prominent example of this is the giant magnetoresistance (GMR), which was first realized by multilayers of alternating nonmagnetic and ferromagnetic metals [1] and which now is an indispensable part of today’s information technology. In these GMR systems the electrical resistance is high for an antiparallel alignment of the magnetization in the neighboring magnetic layers, while it is low for a parallel alignment of those magnetizations. For this reason such systems are also referred to as spin valves.

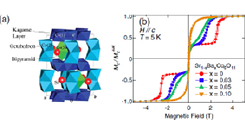
Fig. 1. (a) Crystal structure of SrCo₆O₁₁. (b) Out-of-plane magnetization of Sr_1−xBa_xCo₆O₁₁ as a function of magnetic field (H // c) at 5 K.

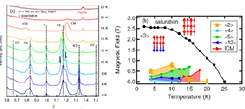
Fig. 2. (a) Magnetic peak profile of SrCo₆O₁₁ at various temperatures at zero magnetic field. (b) Magnetic phase diagram of SrCo₆O₁₁.

Here we report on a high-resolution resonant soft x-ray scattering (RSXS) study of SrCo₆O₁₁ bulk single crystals as a function of temperature (T) and applied magnetic field (H) [2]. SrCo₆O₁₁ is a particularly interesting material with intrinsic magnetoresistance. Figure 1 (a) shows the lattice structure, which is believed to realize a GMR multilayer system at the atomic scale [3]. One of the most striking magnetic features of SrCo₆O₁₁ observed so far are plateaus in the magnetization as a function of the applied magnetic field along the c axis as shown in Fig. 1 (b). These plateaus correspond to 1/3 and 3/3 of the saturated moment and were found to reflect different stackings along c, namely, an up-up-up structure for the 3/3 phase and an up-up-down configuration for the 1/3 phase.

Figure 2 (a) shows the diffraction peaks of SrCo₆O₁₁ at zero field for various temperatures. Quite surprisingly and very uncommon for RSXS experiments, a large number of superlattice reflections at L = n/6 with n = 4, 5, 6, 7, 8 and 9 is observed. L = 1 commensurate (CM) peak and two incommensurate (ICM) peaks around L = 0.8, 1.2 appear at 20 K (T_c1). These ICM peaks move to L = 5/6 and 7/6, respectively, as the temperature is decreased, and finally are locked at these values at 12 K (T_c2), respectively. At T_c2, there appear L = 6/5 and 8/7 shoulders of the L = 7/6, and, simultaneously, L = 2/3, 4/3, and 3/2 peaks. These results therefore directly reveal that a large number of magnetic phases coexist in zero magnetic field.

Figure 2 (b) shows the entire H-T diagram of SrCo₆O₁₁ determined by RSXS measurements under magnetic fields. Here, <n> represents the magnetic periodicities. The phase diagram demonstrates that various magnetic orderings with different periodicities are formed in the low temperature and low field region. Obviously, the energies of these magnetic structures are quite close, and the corresponding energy differences sensitively depend on temperature and magnetic fields. This phenomenon is called “the devil’s staircase,” where, in principle, an infinite number of commensurate superstructures can be realized by tuning an external parameter. As these corresponding eigenstates (magnetic orderings in this case) have similar energies, they can be switched from one to another by small perturbation. In this case of magnetic ordering, the mechanism is described by the axial next-nearest-neighboring Ising (ANNNI) model. The ANNNI model describes competing interactions between nearest (J₁) and next-nearest (J₂) Ising spins, which yields various magnetic orderings with close energies in the phase diagram of temperature and J₂/J₁. However, in order to explain ordered structures with long periodicities, one needs magnetic interactions that go well beyond the nearest neighbors. A plausible explanation can be provided by the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction via the metallic planes.

References

• [1] M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen Van Dau, F. Petroff, P. Etienne, G. Creuzet, A. Friederich, and J. Chazelas, Phys. Rev. Lett. 61, 2472 (1988).
• [2] T. Matsuda, S. Partzsch, T. Tsuyama, E. Schierle, E. Weschke, J. Geck, T. Saito, S. Ishiwata, Y. Tokura, and H. Wadati, Phys. Rev. Lett. 114, 236403 (2015).
• [3] S. Ishiwata, I. Terasaki, F. Ishii, N. Nagaosa, H. Mukuda, Y. Kitaoka, T. Saito, and M. Takano, Phys. Rev. Lett. 98, 217201 (2007).

Authors

• T. Matsuda^a, S. Partzsch^b, T. Tsuyama, E. Schierle^c, E. Weschke^c, J. Geck^b, T. Saito^d, S. Ishiwata^a, Y. Tokura^a,e, and H. Wadati
• ^aDepartment of Applied Physics and Quantum-Phase Electronics Center (QPEC), the University of Tokyo
• ^bLeibniz Institute for Solid State and Materials Research IFW Dresden
• ^cHelmholtz-Zentrum Berlin für Materialien und Energie
• ^dInstitute for Chemical Research, Kyoto University
• ^eRIKEN Center for Emergent Matter Science (CEMS)