Convergence of the Magnetic Grüneisen Parameter at the Quantum Critical Point of the Transverse-Field Ising-Chain
Z. Wang and Y. Kohama
Quantum critical point (QCP) is the end point in a phase diagram where a continuous phase transition occurs at absolute zero temperature. So far, a lot of efforts have been made to understand the universal scaling behavior in different types of QCPs. In case of field-induced QCP, heavy-fermion compound and one-dimensional Heisenberg spin systems are known to show a divergence in thermodynamically properties, such as specific heat and magnetic Grüneisen parameter (Γm). In contrast, for the QCP of the transverse-field Ising (TFI) spin chain system, it is theoretically shown that the Γm does not show a divergence behavior when the QCP is approached by decreasing temperature at the critical field, although it diverges when the critical field is approached at zero temperature [1]. While many theoretical works on the TFI spin chain system are now available, it remains very challenging to experimentally realize the paradigmatic model in a real material.
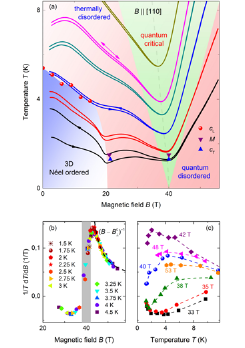
Fig. 1. (a) Magnetocaloric-effect in BaCo2V2O8. The magnetic field was applied to the [110] direction. (b), (c) The estimated Grüneisen parameter, 
, as a function of magnetic field and temperature.
In our recent work [2], we show that the Ising-like spin-1/2 antiferromagnetic chain material BaCo2V2O8 exhibits the unique QCP behavior of the TFI spin system which fulfills the requirements of its experimental observations; (1) strong easy axis anisotropy (2) negligible inter-chain coupling, (3) accessible critical field strength of ~40 T. In this research, we have performed magnetization, sound velocity, and magnetocaloric-effect measurements as a function of temperature and transverse magnetic field on the single crystal of BaCo2V2O8, and have provided the experimental evidence of convergence behavior in Γm. To the best of our knowledge, the Γm above 20 T has been experimentally obtained for the first time in this research, by using the pulsed field magnetocaloric effect (MCE) measurement.
Figure 1(a) shows the magnetocaloric effect data up to 55 T for various initial temperatures. The field dependence of the sample temperature, T(B), detects the 3D Néel ordered phase at about 20 T and the field-induced QCP at 40 T as a broad minimum. The hysteresis below the critical field can be due to slow dynamical process such as field-driven reorientation of twin-domains as reported before. Figure 1(b) and (c) show the temperature and field dependences of 
. Since the T(B) curves was obtained in an approximate adiabatic condition (the sample is thermally isolated due to the extremely short time scale of the pulsed field duration), the process can be considered as an isentropic one. Moreover, the lattice specific heat is not expected to be field dependent. Therefore, the obtained field dependent behavior of corresponds to the Γm = 
. As seen in Fig. 1(b) the field dependence of shows a divergence behavior approaching ~40 T. On the other hand, the temperature dependence of does show a converging behavior at ~40 T with decreasing temperature (Fig. 1(c)). This is consistent with the previous theoretical prediction [1] and the first experimental observation of the characteristic scaling feature in the TFI-chain QCP [2].
References
- [1] J. Wu, L. Zhu, and Q. Si, arXiv:1802.05627 (2018).
- [2] Zhe Wang, T. Lorenz, D. I. Gorbunov, P. T. Cong, Y. Kohama, S. Niesen, O. Breunig, J. Engelmayer, A. Herman, Jianda Wu, K. Kindo, J. Wosnitza, S. Zherlitsyn, and A. Loidl, Phys. Rev. Lett. 120, 207205 (2018).