Spin-ladder systems are a class of low-dimensional materials that correspond to the crossover region between one and two dimensions. The quantum-mechanical properties and criticality of spin-ladder systems have attracted considerable attention. In the S = 1/2 spin-ladder system with the antiferromagnetic Heisenberg (AFH) exchange interaction, it is theoretically predicted that the even-leg spin ladder has a spin gap, while the odd-leg spin ladder is gapless [1, 2]. The spin states of the even-leg AFH spin ladders in the presence of a magnetic field (B) are particularly interesting. There is a transition to a gapless Tomonaga-Luttinger liquid (TLL) phase at a critical magnetic field (B_c1) from a gapped disordered spin liquid state. The quantum critical phenomena are observed in the vicinity of B_c1 as well as another critical field B_c2 at which the spins are fully polarized [3, 4].

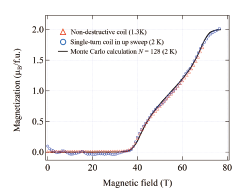
Fig. 1. Magnetization curve of BIP-BNO. The circles and triangles represent the experimental results of the single turn coil and the non-destructive coil, respectively. The solid line shows the numerical result calculated by the quantum Monte Carlo method.

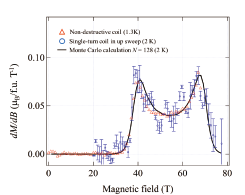
Fig. 2. Magnetic field derivative of magnetization. The solid line, circles, and triangles represent the numerical calculation, experimental result with VSTC, and that with MLPM, respectively. The error bars represent the statistical errors of the experiments of VSTC.

BIP-BNO (3,5’-bis(N-tert-butylaminoxyl)-3’,5-dibromobiphenyl, C₂₀H₂₄N₂O₂Br₂) is a candidate for an S = 1/2 two-leg spin-ladder in which there are no transition metal element but NO groups have S = 1/2 spins [5]. However, since the susceptibility is well reproduced by both a spin-ladder model and a bond-alternating chain model, the key to identify BIP-BNO as a spin-ladder is the magnetization (M) process. In the previous study, the magnetization curve up to 50 T clearly shows the transition at around 35 T. However, the observed magnetization is approximately only up to a quarter of the saturation value M_sat = 2 μB/f.u. To clarify the property of BIP-BNO as a spin-ladder system and to determine accurate exchange constants, it is required to analyze the full magnetization curve and see how well the ladder model can explain the experimental observations.

The measured magnetization curves at low temperatures (1.3 and 2 K) are shown in Fig. 1. The result obtained from a non-destructive-type multilayer-pulsed magnet (MLPM) and that from the destructive-type vertical single-turn coil (VSTC) are represented by triangles and the circles, respectively. Although the pulse duration of VSTC is three orders of magnitude shorter than that of MLPM, the obtained two magnetization curves are found to be almost identical in the field range up to 70 T, which suggests an accurate measurement was conducted not only with non-destructive MLPM but also the destructive VSTC. The magnetization below 37 T is nearly zero reflecting the spin-liquid ground state, which is consistent with the previous study. It is found that the magnetization suddenly starts increasing at 37 T and shows the saturation at fields exceeding 74 T. We expect that the phase in the region where the magnetization is larger than zero and smaller than the saturation value should be the TLL as it is suggested in other two-leg spin-ladder materials. Hence, we find B_c1 = 37 T and B_c2 = 74 T. To compare experimental data with the theoretical model, we calculated the magnetization of the spin-ladder system under a magnetic field by means of the worldline quantum Monte Carlo method with the worm (directed-loop) algorithm. The worm scattering probability is optimized using the geometric allocation. The exchange constants of the model are estimated using the simulated annealing in which the deviation from the experimentally obtained magnetization curve is minimized. The calculated magnetization curve (solid line) is shown in Fig. 1 and we obtain J_rung/kB = 65.7 K and J_leg/kB =14.1 K, where J_rung and J_leg are the exchange constants for the leg and rung directions of the ladder, respectively.

Figure 2 represents dM/dB as a function of B. Sharp two peaks are clearly seen in the numerically calculated as well as experimentally obtained dM/dB curves. Moreover, the inflection point between the two peaks is found to be located at approximately 55 T where M = M_sat/2, and the symmetric form with respect to the inflection point is clearly seen. The symmetric shape in dM/dB is the specific character of a spin-ladder [6]. It should be noted that a bond-alternating chain also give two peaks in the dM/dB curve. However, the shape is distinctly asymmetric; the peak heights of the two are different, e.g., the height of the lower-field peak is from 20 % to 70 % of the height of the higher-field peak, depending on the alternation parameter. Moreover, the inflection point between the two peaks is not at the center position. The difference between the heights of the two peaks in BIP-BNO is evaluated to be only 3% in dM/dB and the inflection point located at the center between the two peaks, which cannot be attributed to a bond-alternating chain. These findings provide strong evidence that BIP-BNO is identified with the S = 1/2 two-leg spin ladder [7].

The ratio of the Heisenberg exchange constants J_rung/J_leg is estimated to be approximately 4.7, which is deeply in the strong coupling region: J_rung/J_leg > 1. In the curve of the magnetic-field derivative of the magnetization, dM/dB, the characteristic features, namely two sharp peaks and a centered inflection point, are observed with a symmetric shape. This observation strongly suggests that BIP-BNO is an S = 1/2 AFH two-leg spin ladder. It is worth noting that BIP-BNO is the first prototypical organic (not containing magnetic ions) S = 1/2 spin-ladder compound.

References

• [1] E. Dagotto, J. Riera, and D. Scalapino, Phys. Rev. B 45, 5744 (1994).
• [2] M. Azuma, Z. Hiroi, and M. Takano, Phys. Rev. Lett. 73, 3463 (1994).
• [3] S. Sachdev, Science 288, 475 (2000).
• [4] B. C. Watson, V. N. Kotov and M. W. Meisel et al., Phys. Rev. Lett. 86, 5168 (2001).
• [5] K. Katoh, Y. Hosokoshi, and K. Inoue et al., J. Phys. Chem. Solids 63, 1277 (2002).
• [6] X. Wang and L. Yu, Phys. Rev. Lett. 84, 5399 (2000).
• [7] K. Nomura, Y. H. Matsuda, and Y. Narumi et al., J. Phys. Soc. Jpn. 86, 104713 (2017).

Authors

• K. Nomura, Y. H. Matsuda, Y. Narumi^a, K. Kindo, S. Takeyama, Y. Hosokoshi^b, T. Ono^b, N. Hasegawa^b, H. Suwa^c, and S. Todo^c
• ^aOsaka University
• ^bOsaka Prefecture University
• ^cThe University of Tokyo