Test of Vacuum Anisotropy under High Magnetic Fields: Vacuum Magnetic Birefringence Experiment
T. Inada, T. Yamazaki, and K. Kindo
Classical electrodynamics governed by Maxwell’s equations describes the vacuum as an isotropic and dispersion-less medium, which properties are not affected by the application of electromagnetic fields. However, if we consider quantum electrodynamics (QED), the nonlinear interaction between the fields is mediated by the vacuum fluctuation of virtual particle-antiparticle pairs. Consequently, the vacuum shows a finite size of anisotropy under strong magnetic fields, called vacuum magnetic birefringence (VMB). In addition to this QED effect, VMB can be enhanced by the contribution from undiscovered particles such as axions, which are one of the leading candidates of dark matter. The test of VMB therefore provides one of the most sensitive searches for these particles with a mass around meV.
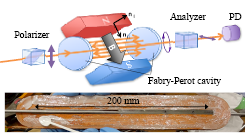
Fig. 1. (upper) Schematic veiw of the setup. An incident light is polarized and stored in a high-finesse Fabry-P´erot cavity, where pulsed magnetic fields induce elliptical polarization. (lower) Bare racetrack coil before backed up with an outer metal. The magnet produces fields of up to 10 T over the beam path.
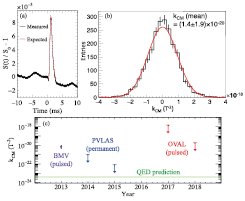
Fig. 2. (a) Test measurement of the small square term of the Faraday effect caused by 100 Pa of nitrogen gas, compared to calculation. The vertical axis shows the ratio of signal height with respect to the static component S0. (b) Histogram of vacuum ellipticity coeffcient kCM obtained by 2000 cycles of alternating +9 T and −4.5 T fields. The fitting to a Gaussian distribution shows a zero-consistent value for the mean, which gives an upper limit on kCM. (c) Comparison of the current limits on kCM (OVAL) with the other two groups. Note that, without hypothetical particles such as axions, QED alone predicts finite vacuum birefringence shown as the green line.
Three groups are currently trying to measure VMB, with a common scheme shown in Fig. 1. It consists of crossed-Nicols polarizers, a high-finesse Fabry-P´erot cavity, and a magnet that applies transverse fields with respect to the laser axis. The VMB signal is measured as ellipticity induced by the magnet. The surface of cavity mirrors has large static birefringence, and to separate the VMB signal from it, magnetic fields are temporally modulated. The modulation is realized by a rotating permanent magnet (∼ 2.5 T) by one of the groups, whereas we instead use a pulsed magnet since the VMB signal is enhanced according to the square of the field strength (B2). Our magnet produces alternative fields of +9 T and −4.5 T with a high repetition rate of 0.1 Hz [1, 2].
The sensitivity to VMB is determined by the background process of the Faraday effect caused by residual gas in the chamber. Since the Faraday component is linearly depends on B, we apply alternative fields to subtract it. To emulate the B2 dependence of the small VMB signal, we first filled a relatively high pressure of nitrogen gas (100 Pa) and observed the square term of linear Faraday effect. Figure 2(a) shows the agreement of the measured B2 term with calculation of the squared Faraday term. The VMB measurement was then carried out under vacuum with ∼ 2000 cycles of the alternating fields in 2018. The VMB coeffcient kCM is calculated for each cycle and distributed as shown in Fig. 2(b). The mean value of the distribution is consistent with zero, showing no sign of axionic contribution. As a result, it poses an upper limit on kCM, that is plotted in Fig. 2(c) with recent results of the other groups. We have improved our first result in 2017 by two orders of magnitude [3]. There is still a large gap of sensitivity to reach the signal level predicted by QED, and upgrades on the magnet and optics are currently underway.
References
- [1] T. Inada et al., Phys. Rev. Lett. 118, 071803 (2017).
- [2] T. Yamazaki et al., Nucl. Instrum. Methods Phys. Res. A 833, 122 (2016).
- [3] X. Fan et al., Eur. Phys. J. D 71, 308 (2017).
