Spin Singlet Orders in Breathing Pyrochlores
Tsunetsugu Group
Geometrically frustrated magnets are a good playground in the quest for new quantum phases of matter, and kagome and pyrochlore magnets are their representatives. A few years ago, Okamoto et al. [1] discovered an unidentified phase transition in the spinel variety Li(Ga,In)Cr4O8, in which the magnetic Cr ions form a breathing pyrochlore lattice, and this has motivated a theoretical investigation of its origin.
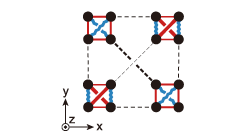
Fig. 1. Nearest-neighbor spin correlations in the breathing-pyrochlore Heisenberg model with S = 3/2. Four squares depict small tetrahedron units in the cubic unit cell projected onto the xy plane. In each unit, antiferromagnetic correlations are shown by red bonds and their width schematically shows |Si・Sj|, while blue bonds show ferromagnetic correlations. Dashed lines show weak antiferromagnetic correlations between neighboring units.
The breathing pyrochlore lattice is a staggered network of corner-sharing tetrahedrons with two sizes, and increasing In concentration enhances the size difference. The antiferromagnetic Heisenberg Hamiltonian is a minimal model to study magnetic properties in this compound, and this requires two values of nearest-neighbor exchange coupling J’≪J corresponding to different tetrahedron units. This model was theoretically studied for the case of spin S = 1/2 [2] and it was predicted that the spin gap is finite and the ground state exhibits a complicated spatial modulation without breaking spin rotation symmetry. Among the four sublattices of small tetrahedra, three of them show dimer-pair orders of different pairing combination, and the remaining sublattice shows either a dimer-pair order or a tetramer order. Considering Cr3+ ions have a spin S = 3/2, the important issue is if this larger spin changes an order in the ground state.
To study this problem, I have developed a systematic scheme of degenerate perturbation theory for the breathing pyrochlore Heisenberg model with general spin S, and derived an effective Hamiltonian for describing dynamics in the spin singlet subspace. The effective Hamiltonian is in the order of (J’/J)3 and represented in terms of spin-pair operators τ, and we have studied its ground state by a mean field approximation [3]. The operators are defined in the local singlet space with dimension 2S + 1 at each small tetrahedron, and we have solved the challenge of calculating their matrix elements for general S. It turns out that an essential difference from the S = 1/2 case is the presence of Z3 anisotropy in the internal τ space, and this stabilizes a different order. The anisotropy grows for larger S and inherits the cubic symmetry of the lattice structure. Two sublattices of small tetrahedrons now show an identical tetramer order, and the other two sublattices show another tetramer order with a small distortion. We have analyzed the spin correlations in this new ordered state in detail for S = 3/2 and 1, and calculated the equal-time spin structure factor S(q). The amplitudes of the components breaking the cubic lattice symmetry in S(q) are calculated and they can be used to determine the value of J’/J. It shall be interesting to verify this scenario by carrying out a neutron scattering experiment and compare its results with this prediction.
References
- [1] Y. Okamoto, G. Nilsen, T. Nakazono,and Z. Hiroi, J. Phys. Soc. Jpn. 84, 043707 (2015).
- [2] H. Tsunetsugu, J. Phys. Soc. Jpn. 70, 640 (2001); Phys. Rev. B 65, 024415 (2001).
- [3] H. Tsunetsugu, Prog. Theor. Exp. Phys. 2017, 033101 (2017).
