Development of Numerical Library Kω ver. 1 and Quantum Lattice Solver HΦ ver. 2
T. Hoshi and Y. Yamaji
The two novel open-source softwares of (i) numerical library Kω ver.1 [1] and (ii) quantum lattice solver HΦ ver.2 [2] were developed in Project for advancement of software usability in materials science [3] at the fiscal year of 2016. The project name is ‘shifted Krylov-subspace algorithm and novel solvers for computational condensed matter physics’. The project is an interdisciplinary one between computational material science and applied mathematics. The softwares are preinstalled on the supercomputer (sekirei) at ISSP [3]. The two softwares are closely related, because Kω is a set of numerical linear-algebraic routines and HΦ ver.2 supports the use of Kω in the optical spectrum calculations.
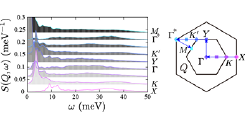
Fig. 1. Calculated dynamical structure factors S(Q, ω) of Na2IrO3 [8]. The spectra are vertically shifted depending on Q. The Brillouin zone of Na2IrO3 is shown in the right panel.
Kω is a general numerical library for the Green’s function of Gab(ω) = <a | [(E0 + ω + iδ)I − H]-1 | b> , where H is a large scale complex Hermitian or real-symmetric matrix and |a>, |b> are the input vectors. Traditionally, the problem was solved by the Lanczos-based algorithm. In the present solver, instead, the numerical solution is obtained from the linear equation of [(E0 + ω + iδ)I − H] | x > = | b > and the solution of | x > is obtained by the novel iterative algorithm, called shifted Krylov subspace algorithm [4,5]. The algorithm was used for the excited spectrum of many-body states in a previous paper [5], which motivated us to the present project. The algorithm enables us to control the accuracy of the spectrum Gab(ω) at a specific frequency ω, when one monitors the residual vector. The method is general and was applied also to many other computational science fields, such as QCD [4], electronic structure calculations, transport calculation with non-equilibrium Green’s function theory. Kω is a general numerical library and can be called, in principle, from any material simulator, as well as HΦ ver.2. Moreover, a mini application is included in the package of Kω, so that researchers can evaluate the numerical library before the use in their real researches.
HΦ ver. 2 is the latest version of HΦ [6]. The quantum lattice solver HΦ is a program package based on exact diagonalization applicable to a broad range of quantum lattice models, including the Heisenberg model, the Kitaev model, the Hubbard model and the Kondo-lattice model. In HΦ ver. 1, the Lanczos method for calculating the ground state and a few excited states, thermal pure quantum (TPQ) states [7] for finite-temperature calculations, and full diagonalization method for checking results of Lanczos and TPQ methods are implemented with an easy-to-use and flexible user interface. The project in the 2016 fiscal year [3] has supported implementation of the Lanczos and shifted Krylov-subspace algorithm for calculating excitation spectra in the latest version HΦ ver.2. The HΦ ver.2 call subroutines for the shifted Krylov-subspace algorithm from the library Kω.
As an example tractable by HΦ ver.2, we show excitation spectra of an ab initio spin hamiltonian of an iridium oxides Na2IrO3 [8], which is a so-called Kitaev material and a typical example of frustrated magnets due to magnetic anisotropy. In Fig.1, dynamical spin structure factors calculated for a 24-site cluster of the ab initio spin hamiltonian of an iridium oxides Na2IrO3 are shown. The continuum in the spectra is the hallmark of the proximity to the Kitaev’s quantum spin liquid. The controlled accuracy of the shifted Krylov-subspace algorithm safely resolves the detailed continuum spread over the wide range of frequency, where the typical exchange energy scale of Na2IrO3 is 30 meV.
References
- [1] https://github.com/issp-center-dev/Komega
- [2] https://github.com/QLMS/HPhi
- [3] http://www.issp.u-tokyo.ac.jp/supercom/softwaredev
- [4] A. Frommer, BiCGStab(l) for families of shifted linear systems, Computing 70, 87 (2003).
- [5] S. Yamamoto, T. Sogabe, T. Hoshi, S.-L. Zhang and T. Fujiwara, J. Phys. Soc. Jpn. 77,114713 (2008).
- [6] M. Kawamura, K. Yoshimi, T. Misawa, Y. Yamaji, S. Todo, N. Kawashima, Computer Physics Communications (to be published).
- [7] S. Sugiura and A. Shimizu, Phys. Rev. Lett. 108, 240401 (2012).
- [8] Y. Yamaji, Y. Nomura, M. Kurita, R. Arita, and M. Imada, Phys. Rev. Lett. 113, 107201 (2014).
