Compressed Sensing in Scanning Tunneling Microscopy/Spectroscopy for Quasi-Particle Interference
Y. Nakanishi-Ohno, Y. Yoshida, and M. Okada
Interference of electrons is one of the manifestations of their particle-wave duality in quantum mechanics. When electrons are scattered by local disordered structures, such as adsorbates and step edges on surfaces, the reflected electronic wave interferes with the injected one to form a spatial modulation in local density of states (LDOS), that is, a quasi-particle interference (QPI) pattern. The modulated LDOS can be observed in real space by using scanning tunneling microscopy and spectroscopy (STM/S) at various energies around the Fermi level, and by analyzing a QPI pattern one can obtain the momentum (k) space information on the electronic states and their energy dispersion relation. Recently, the QPI analysis has been applied to investigate electronic structures of complex materials such as unconventional superconductors and topological insulators. As the measurements can be performed at very low temperature under high magnetic fields, the method is a powerful tool in various aspects of solid state physics.
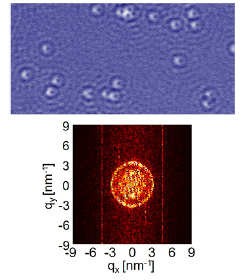
Fig. 1. (upper) dI/dV map taken on the Ag(111) surface. The size of the area is 70 nm × 35 nm, and the number of pixels is 360 × 180 = 64800 points. (lower) FT of the upper STM image by the conventional method.
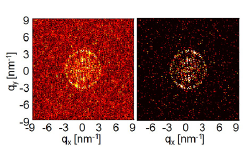
Fig. 2. FTs estimated from pixels randomly chosen from the dI/dV mapping shown in the upper panel of Fig. 1. The subsets of data are composed of 7200 pixels. Results of the conventional method and LASSO are shown in the left and right panels, respectively.
In order to obtain the energy dispersion relation of electronic states, however, the spectrum of tunneling conductance dI/dV, which corresponds to LDOS, has to be taken at every pixel while scanning. It is therefore quite time-consuming; sometimes it takes more than a week, which makes the QPI measurements difficult to be performed. If one can obtain the same quality of the k-space information from a reduced number of spectra, the QPI analysis will be much more convenient and widely used.
As a solution to the problem posed above, we have applied compressed sensing (CS) to the QPI observation, which is a novel statistical method for acquiring and reconstructing a signal efficiently. In the case of QPI observation, the k-space information on the electronic states is obtained by performing the Fourier transformation (FT) of the QPI pattern. If the number of dI/dV spectra is decreased, the FT of the dI/dV map becomes of too low quality to access the k-space information. In order to boldly enhance the resolution of k space, we need to solve an underdetermined problem, in which the number of variables measured is smaller than the number of variables to be determined. CS addresses this problem by utilizing the sparseness of QPI patterns; their FTs are composed of few nonzeros and many zeros. This sparseness is based on the fact that LDOS modulations are allowed only for a small number of wavelengths. Because of this sparseness, we can reduce the number of unknown variables significantly, and then obtain an FT of sufficient quality even with scarce data.
Here, we demonstrate that CS performs well by numerical simulations on a QPI pattern observed in a dI/dV map of the Ag(111) surface. The surface state of Ag(111) is described by a free-electron-like model, and the FT of the QPI pattern has a circular pattern whose radius corresponds to twice the wavenumber of the states. We use an analysis method of CS, called LASSO (least absolute shrinkage and selection operator), to recover the pattern from scarce data.
Figure 1 shows a dI/dV mapping (360 × 180 = 64800 pixels) taken on the Ag(111) surface at 4.2 K. The mapping shows a wave-like QPI pattern around adsorbates on the surface. The FT of this dI/dV map obtained by the conventional method is shown in the lower panel of Fig. 1. A ring structure can be seen centered at the origin, indicating the presence of isotropic electronic states on the surface. We also found small intensity other than the ring, supporting the assumption of sparseness. The q-space region of interest is discretized into 128 × 128 = 16384 pixels. In this case, the amount of data is enough sufficient compared to the number of unknown variables.
Let us examine whether the circle can be recovered from a reduced amount of data. Figure 2 shows FTs of 16384 pixels, which are estimated from data of 7200 points randomly chosen from the dI/dV mapping shown in Fig. 1. It should be noted that the number of unknown variables is larger than that of the measured variables. The left and right panels show the results of the conventional method and those of LASSO, respectively. Although the ring pattern can be seen in the FT by the conventional process (left panel), it has rather noisy background because of the reduced amount of data. On the other hand, the analysis with LASSO significantly reduces the background noise, and the expected pattern is more clearly seen in the result (right panel). In the ill-posed situation, LASSO provides a sparse solution; most of the noise components are automatically estimated at zero, and the signal components remain to be nonzero. Our numerical simulations demonstrated that LASSO enables us to recover the characteristic features of the electronic states of Ag(111) surface from a randomly reduced dataset. Our results indicate that CS works effectively in the analysis of QPI, saving the number of required dataset and measurement time, which improve the efficiency of the QPI analysis. Obviously the application of CS should not be limited to the QPI analysis; we expect that it will be extended more to various situations in condensed matter physics near future.
References
- [1] Y. Nakanishi-Ohno, M. Haze, Y. Yoshida, K. Hukushima, Y. Hasegawa, and M. Okada, J. Phys. Soc. Jpn. 85, 093702 (2016).
