Absence of Superconductivity in the Collapsed Tetragonal Phase of KFe2As2 under Hydrostatic Pressures
Uwatoko Group
High pressure phase diagram of the tetragonal KFe2As2 remains controversial because of the strong sensitivity of superconducting transition temperature (Tc) depending on the type of the pressure cells and the pressure transmitting medium. Specially, the superconductivity of the collapsed tetragonal KFe2As2 is an open question since there are no zero resistivity state in the previous studies [1-3], presumably due to the pressure inhomogeneity or the non-hydrostaticity. To resolve these issues pertaining to this intriguing compound, we studied the temperature dependence of resistivity on KFe2As2 single crystals down to 20 mK under various much improved hydrostatic pressures up to 17.5 GPa generated in a cubic anvil cell.
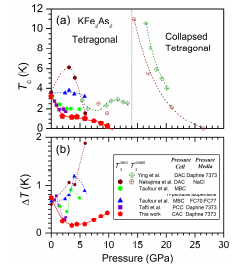
Fig. 1. (a) Temperature-Pressure phase diagram of KFe2As2 a. The solid and open symbols represent the zero resistivity state temperature Tczero and the onset temperature Tconset of superconducting transition, respectively. (b). ΔTc (= Tconset - Tczero) as a function of pressure. “DAC”, “MBC”, “PCC”, “CAC” represent diamond anvil cell, modified Bridgeman method, piston cylinder cell, and cubic anvil cell, respectively.
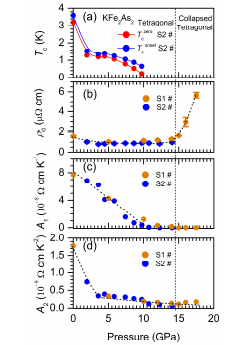
Fig. 2. The evolutions of parameters under pressure: (a) Tconset and Tczero; (b) ρ0; (c) A1; (d) A2. The dashed line indicated phase transformation at lower temperature.
Figure 1 shows the superconducting phase diagram and the superconducting transition widths of KFe2As2under pressure with the previous data for comparison. Pressure dependence of Tc has several distinct features: firstly, superconducting transition width ΔTc becomes much narrower in the same pressure region. As the pressure increases, ΔTc decreases and is ~ 0.2 K for 1.9 < P < 5.8 GPa; and zero resistivity state retains up to 11 GPa where the superconducting state disappears. While in other reports, the superconducting transition becomes broad evidently as the pressure increases and ΔT increases to ~ 0.5-2 K depending on the pressure apparatus; zero resistivity state cannot be achieved above 7 GPa. Secondly, Tc obtained is lower than others in the same pressure regions in Fig. 1(a). As proposed, Tc of tetragonal KFe2As2 depends sensitively on pressure conditions and was enhanced if under a less hydrostatic condition [3]. These characteristic suggests a much improved hydrostatic pressure condition in a cubic anvil cell in comparison with the piston cylinder cell (PCC) or diamond anvil cell (DAC) under higher pressure. We examined the resistivity of KFe2As2 in the pressure region of 14 < P < 17.5 GPa, however, superconductivity does not appear down to 2 K, which are contrary to the previous results using DAC [1,2]. In striking contrast to previous reports in Fig. 1, no superconducting phase emerges upon further increasing pressures until the collapsed tetragonal KFe2As2 forms and it was argued that such a discrepancy can be attributed to the different pressure apparatus or homogeneity.
We studied the temperature dependence of resistivity ρ(T) under pressures by adopting an empirical formula ρ = ρ0 + A1T + A2T2 to construct a qualitative relation between the evolution of temperature coefficient and the Tc. Here, the T2 term is to describe the Fermi liquid state and the T-linear term is associated with the electronic correlations and scattering process such as the electron-boson interaction and/or critical fluctuations near QCP. The parameters were presented Fig. 2. The residual resistivity ρ0 decreases monotonically, and starts to increases at 14 GPa, then jumps to nearly three times with the pressure increasing up to 17.5 GPa, which is sharply different from the reports by using DAC [1]. As the pressure increases, A1 decreases linearly and becomes almost zero around 11 GPa, coinciding with the suppression of Tc. This close connection between Tc and A1 suggests that the scattering mechanism leading to the T-linear term play an important role for the appearance of SC in KFe2As2. On the other hand, A2 decreases rapidly with approaching Pc1, and then gradually decreases with further increasing pressure. Furthermore, this observation is in agreement with a magnetic quantum critical point located at a negative pressure [4]. Incidentally, the shallow minimum of Tc near ~ 2 GPa is not explicable in terms of the pressure dependence of A1 and A2. Other factors such as pressure variation of the density of state at the Fermi level, balance between intra- and inter-Fermi-surface-pockets scattering affect Tc. The combined interplays of those factors would be important to fully understand the evolution of Tc under pressure.
References
- [1] Y. Nakajima, et al., Phys. Rev. B. 91, 060508 (R) (2015).
- [2] J. J. Ying et al., arXiv: 1501.00330 (2015).
- [3] V. Taufour, et al., Phys. Rev. B 89, 220509(R) (2014).
- [4] P. S. Wang, et al., Phys. Rev. B. 93, 085129 (2016).
