Helical Magnetism in the Vicinity of the Superconducting State in MnP
Uwatoko, Kato, and Sugino Groups
MnP exhibits superconductivity under pressure with a maximum transition temperature of ~1 K at 8 GPa [1]. Since Mn has the spin degree of freedom, elucidating the magnetic contribution to the superconductivity is crucial to understand the pairing mechanism. In particular, the magnetic state in the vicinity of the superconducting phase needed to be clarified. In order to study the pressure dependence of the magnetic ground state in MnP, high pressure neutron diffraction measurements were performed up to 3.8 GPa [2]. The high pressures below and above 2 GPa were generated with a self-clamped piston-cylinder cell and a palm cubic anvil cell, respectively.
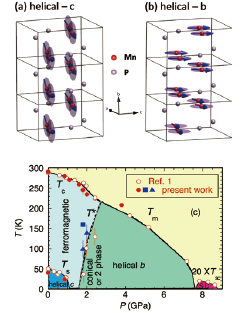
Fig. 1. Helical spin structures under low (helical-c) (a) and high pressures (helical-b) (b). (c) Temperature-pressure phase diagram. The open and filled symbols represent the data in Ref. 1 and the present results, respectively. The filled square is the temperature where the incommensurate magnetic peaks start to develop. The filled triangles are the temperatures where the commensurate magnetic signal starts to decrease.
MnP shows a ferromagnetic order below Tc ~ 290 K followed by a helical order (helical-c, Fig. 1a) with the spins lying in the ab plane and the helical rotation propagating along the c axis below Ts ~ 50 K at ambient pressure [3,4]. With increasing pressure, we found that both Tc and Ts are gradually suppressed and the helical order disappears at ~1.2 GPa. At intermediate pressures of 1.8 and 2.0 GPa, the ferromagnetic order first develops and then is suppressed at a lower temperature (T*). New incommensurate magnetic peaks split along the b axis appear below T*. The new magnetic peaks originate from another helical structure, which hosts the spins in the ac plane and the propagation along the b axis (helical-b, Fig. 1b). Since the ferromagnetic component still remains, the magnetic ground state is a conical or two-phase (ferromagnetic and helical-b) structure. Above 2 GPa, a magnetic transition from paramagnetic directly to the helical-b states appears below Tm. The magnetic phase diagram is shown in Fig. 1c. The magnetic state close to the superconducting phase was found to be the helical-b structure.
In the helical-b phase, the helical transition temperature and the ordered moment decrease with increasing pressure. On the other hand, the magnetic incommensurability becomes larger with increasing pressure, indicating that antiferromagnetic interactions become more dominant than ferromagnetic ones, which are influential at low pressures. This suggests that antiferromagnetic fluctuations might be connected to the superconducting pairing mechanism in MnP.
At ambient pressure, MnP is considered to be a localized d electron spin system of Mn, interacting with itinerant s electrons of P, which is reproduced by the s-d model. Applying pressure causes more enhanced orbital overlap between Mn atoms, which gives rise to more itinerancy. The density-functional theory (DFT) calculation shows that the pressure gradually reduces the Mn moments and finally leads to a nonmagnetic state [5]. The Mn moment estimated at 3.8 GPa and 5 K is 0.84(14)μB, which suggests that the lattice compression is very close to the critical regime where the large d-d overlapping makes the system more itinerant and the spontaneous magnetization does not occur [5]. In Ref. 5, only collinear spin structures (one ferromagnetic and three antiferromagnetic structures) are considered as potential ground states. The ferromagnetic structure was found to be most stable in MnP until the magnetic moment disappears with compression. This result does not exclude the possibility of a noncollinear magnetic state between ferromagnetic and itinerant nonmagnetic states. Further theoretical studies on the magnetic state in the vicinity of the itinerant nonmagnetic state are desirable.
References
- [1] J.-G. Cheng, K. Matsubayashi, W. Wu, J. P. Sun, F. K. Lin, J. L. Luo, and Y. Uwatoko, Phys. Rev. Lett. 114, 117001 (2015).
- [2] M. Matsuda, F. Ye, S. E. Dissanayake, J.-G. Cheng, S. Chi, J. Ma, H. D. Zhou, J.-Q. Yan, S. Kasamatsu, O. Sugino, T. Kato, K. Matsubayashi, T. Okada, and Y. Uwatoko, Phys. Rev. B 93, 100405(R) (2016).
- [3] G. P. Feicher, J. App. Phys. 37, 1056 (1966).
- [4] J. B. Forsyth, S. J. Pickart, and P. J. Brown, Proc. Phys. Soc. 88, 222 (1966).
- [5] Z. Gercsi and K. G. Sandeman, Phys. Rev. B 81, 224426 (2010).
